浮力と慣性力の比を表した無次元数です。
重力加速度を g [m/s²]、体膨張係数を β [1/K]、代表温度差を ΔT [K]、代表長さを L [m]、代表速度を U [m/s] とすると、リチャードソン数 Ri は以下の式によって求められます。

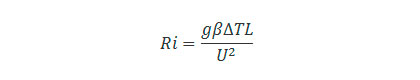
リチャードソン数は流れ場において、自然対流と強制対流のどちらが卓越するかを表したものです。この値が大きい場合には自然対流が、小さい場合には強制対流が卓越することを示しています。
なお、リチャードソン数という名前はイギリスの数学者 ルイス・フライ・リチャードソンにちなんだものです。

※本計算ツールは、無償で提供するものですので、その品質や性能についていかなる保障もされておりません。したがって、利用者は自己の責任において使用することとし、使用することで生じた損害の一切の責任を弊社は負いません。