6.2.2 差分法

　差分法 （Finite Difference Method: FDM）は、解析空間に離散点を配置して、微分（関数の傾き）を差分商によって近似する方法です。差分商とは、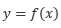 という関数において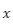を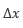変化させたときの  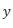の変化が 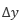 である場合の  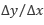のことです。本来の微分の定義は　

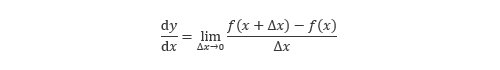
という式で表されますが、差分商はこの式において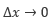の極限を取らない、すなわち有限の区間の傾きを考えることに相当します。これを式で表すと以下のようになります。

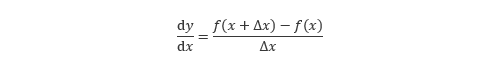
　それでは、図を見ながら確認していきましょう。図6.5の赤線で示した関数を考えると、点Aにおける微分は図中に「本来の傾き」と示した黒線となります。これを点AとBの値を用いた差分商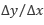 で近似することは、傾きを図6.5 (a) の青線で表すことに相当します。また、点Bの代わりに点Aとの距離がより近い点B’の値を用いると、図6.5 (b) の青線のように先ほどより本来の傾きに近い結果を得られます。このように、計算に用いる2点の間隔が小さいほどより良い近似となります。

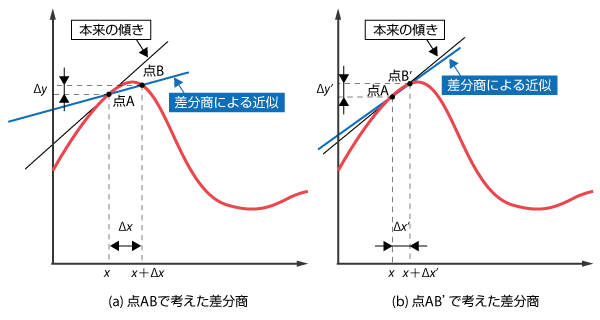
図6.5　微分の差分近似（前進差分）

　ところで、差分商の計算に用いる点の選び方には任意性があります。図6.5のように点Aから見て前寄りの点を用いる差分を 前進差分 といいます。これに対して、図6.6 (a) に示すように点Aから見て後寄りの点を用いる差分を 後退差分、図6.6 (b) のように前後両側の点を均等に用いる差分を 中心差分 といいます。

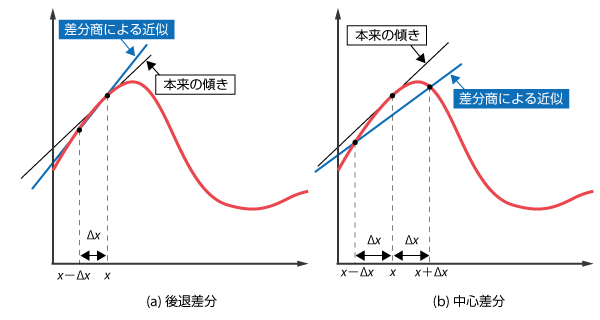
図6.6　後退差分と中心差分

なお、図6.6の後退差分と中心差分を式で表すと、以下のようになります。

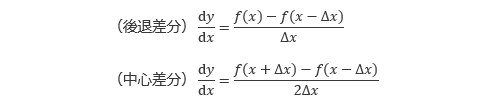
　差分法は勾配の計算に用いる点の数を増やしていくことで容易に高精度化できるという長所があります。その一方で、計算点が規則的に並んでいる必要があるため、計算対象の形状が複雑な場合には適用が難しいという短所があります。そのため、大学や研究機関などの学術計算のように、形状が比較的単純で高い計算精度が要求される計算に対して用いられることが多い手法となります。

 もっと知りたい  　差分近似の精度

　上で述べたような差分近似はあくまでも近似なので、元の微分とは厳密には一致しません。この差のことを 離散化誤差 といいます。この離散化誤差の大きさは テイラー展開 を用いて評価することができます。例えば、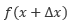 を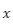におけるテイラー展開で表すと以下の式が得られます。

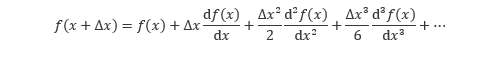
この式を変形すると、以下のように書き換えられます。

右辺の第1項が前進差分そのものであるため、微分を前進差分で近似した場合には、右辺第2項以降を誤差として生じることになります。この誤差のうち、最も主要な項は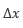 の１乗に比例する項であるため、この前進差分は１次精度前進差分と呼ばれます。同様にテイラー展開を用いることで、前述の後退差分と中心差分はそれぞれ１次精度と２次精度と分かります。１次精度であれば、離散化の幅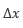を1/2にすると誤差は1/2に、２次精度では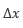を1/2にすると誤差が1/4になります。このように○次精度の数字が大きいほど、分割を細かくしたときの誤差の減り方が大きく、精度が高い近似ということになります。

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。執筆したコラムに「流体解析の基礎講座」がある。　 　

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください