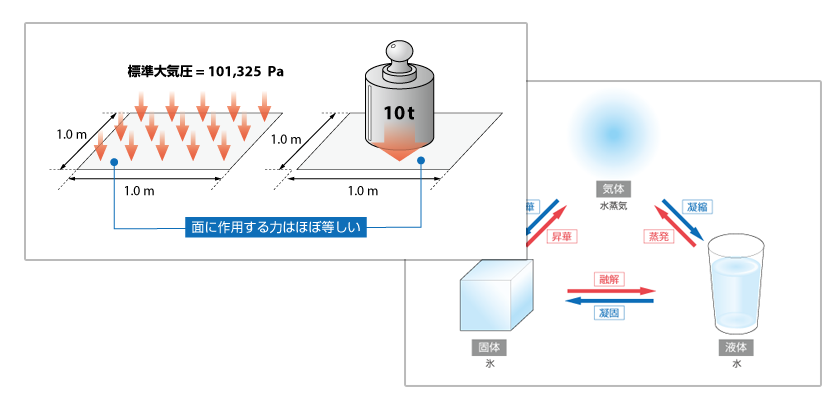
7.3.2 ラージエディシミュレーション (1)

　現実の流れ場には大小さまざまな 渦 が存在しています。このとき、乱流渦が持つエネルギーと乱流渦の波数（乱流渦の直径の逆数）を両対数グラフに示すと図7.14のようになります。

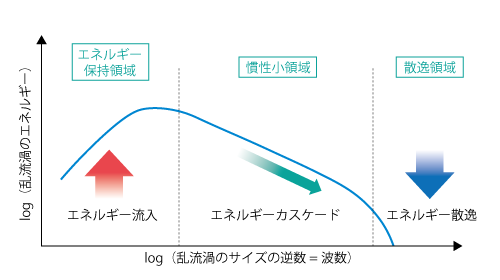
図7.14　乱流渦が持つエネルギー

上の図は右に進むほど小さな渦を表しており、その大きさに応じて、エネルギー保持領域・慣性小領域・散逸領域 の三つの領域に分けられます。それぞれの領域に属する渦を模式的に示すと図7.15のようになります。

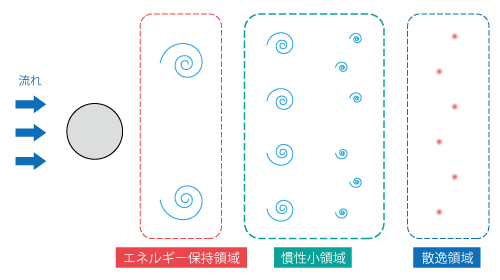
図7.15　乱流渦のサイズの模式図

　これらの渦のうち、エネルギー保持領域に属する大きな渦は、流れ場に存在する物体の影響を強く受けたスケールであるため、その性質が流れ場によって大きく異なります。一方で、慣性小領域や散逸領域に属する小さな渦は、大きな渦が分裂する過程で流れ場に依存した性質が失われるため、大きな渦に比べると普遍性を有することが知られています。

そこで、流れ場ごとの依存性が顕著である大きな渦のみを直接計算し、それ以外の小さな渦はモデル化するという方法が考えられます。このような方法を ラージエディシミュレーション、またはその英語表記（Large Eddy Simulation）の頭文字を取って LES といいます。LESによるモデル化のイメージを示すと、図7.16のようになります。

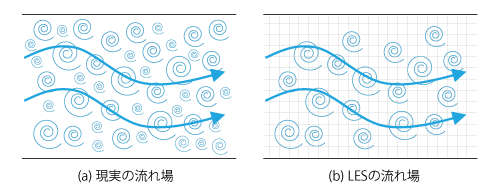
図7.16　LESによるモデル化

　LESでは、直接計算される大きなスケールのことを グリッドスケール（grid scale, GS）、モデル化される小さなスケールのことを サブグリッドスケール（subgrid scale, SGS）といいます。これらのイメージを示すと図7.17のようになります。

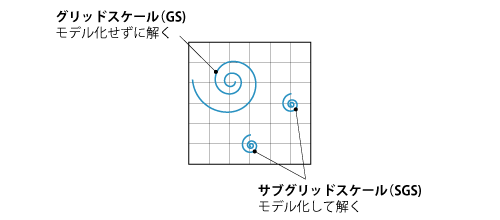
図7.17　グリッドスケールとサブグリッドスケール

　両者の区別は メッシュ とは独立したフィルターサイズによって任意に決められますが、メッシュの性能をもっとも発揮できるのはフィルターとメッシュのサイズを一致させたときであるため、メッシュサイズをフィルターサイズとするのが一般的です。

また、LESは空間的なフィルター操作による平均化であることから 空間平均モデル とも呼ばれます。なお、これに対して RANS のことを 時間平均モデル と呼ぶことがあります。LESはRANSとは異なり、時間方向の平均化は行っていないため、非定常解析 が必須となります。

　メッシュのサイズに関係なく、あらゆる乱れがモデル化されるRANSとは異なり、LESではフィルターサイズ、すなわちメッシュサイズに応じたモデル化が行われます。この関係を示したものが図7.18です。したがって、LESとして意味のある計算を行うためには、メッシュの大きさに注意を払わなければいけません。

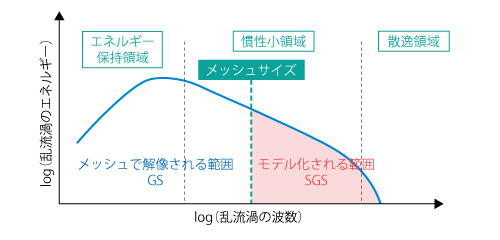
図7.18　乱流渦が持つエネルギーとメッシュサイズの関係

図7.18を模式図で示すと、図7.19のようになります。

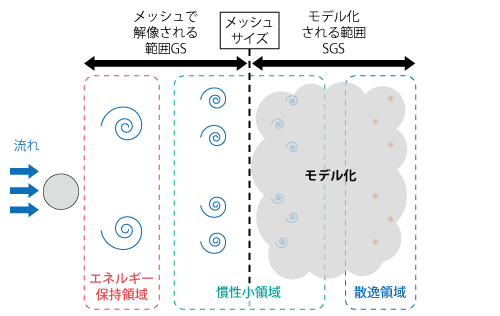
図7.19　モデル化される範囲の模式図

　LESは普遍性が期待できる小さな渦、すなわち慣性小領域や散逸領域の渦をモデル化し、エネルギー保持領域の渦をメッシュで解像することを前提にした手法です。したがって、その趣旨に沿った計算を行うためには、図7.18や図7.19に示す程度と同等、もしくはそれより小さいメッシュサイズにすることが望ましく、その場合の計算負荷はRANSと比較して格段に大きくなります。

仮に、メッシュサイズを大きくしたとしても計算自体は行えますが、図7.19でモデル化される範囲が大半を占めるという状況となるため、実質的にはLESとは呼べない計算となってしまいます。

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。執筆したコラムに「流体解析の基礎講座」がある。　 　

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください