7.3.1 レイノルズ平均モデル (2)

　前回示した RANS の 基礎方程式 を改めて以下に示します。

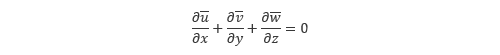
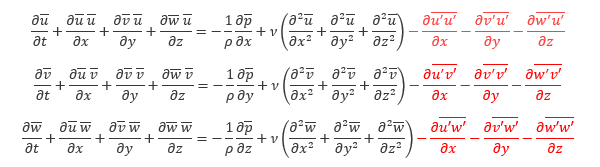
RANSを用いたモデル化によって現れるのが赤字で示した レイノルズ応力 です。

　ここで問題となるのが、レイノルズ応力以外の項は速度の時間平均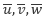（）を用いた表現となっているのに対し、レイノルズ応力は変動量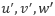（）を用いた表現となっているため、方程式が閉じておらず（未知数の数 > 方程式の数）、このままでは計算できないという点です。

また、レイノルズ応力を何らかの方法で解こうとすると、ナビエ・ストークス方程式 の非線形性に起因した未知の相関が際限なく続いて解くことができません。したがって、これを解くためには、既知の変数を用いてレイノルズ応力を近似し、計算可能な表現に書き換える必要があります。この手続きを 完結 や クロージャ（closure）といい、その際の近似に用いられるものが狭義の 乱流モデル となります。

　さて、代表的なモデルの一つに、不規則な乱流渦によって生じるレイノルズ応力を分子粘性によって生じる 粘性応力 との類推から与えるモデルがあります。このようなモデルを総称して 渦粘性モデル といいます。

3.3.1節 で示したように、分子粘性による粘性応力は 粘性係数 と 速度勾配 の積によって表されますが、渦粘性モデルではレイノルズ応力が「乱流渦に伴う拡散係数」と「平均速度の勾配」の積によって表されると考えます。このモデル化された拡散係数のことを 渦粘性係数 といい、両者の対比を クエット流れ を用いて示すと図7.7のようになります。

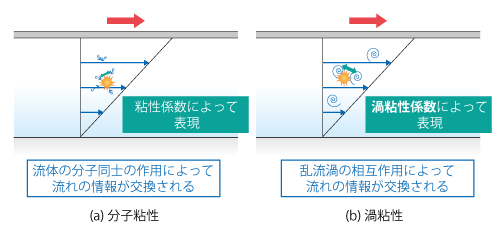
図7.7　分子粘性と渦粘性の対比

　計算は 流体 の 物性値 である粘性係数に渦粘性係数を加えて行われ、乱れが大きくなるほど流れの抵抗が大きくなるというモデル化になります。流れを人の動きに例えると、図7.8に示すように、人が規則正しく歩いているところは「抵抗が小さく歩きやすい」、人がばらばらの向きや速度で動いているところは「抵抗が大きく歩きにくい」というイメージです。

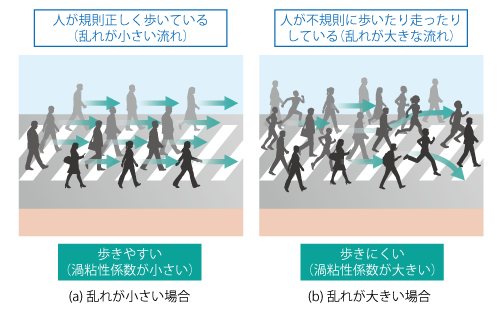
図7.8　乱れによる抵抗のイメージ

　渦粘性モデルを導入することで、レイノルズ応力は渦粘性係数と平均速度の勾配を用いて表現できるようになります。しかし、流体に固有の物性値である粘性係数とは異なり、渦粘性係数は流れの状態によって決まる物理量であるため、その値は一定ではありません。

また、渦粘性係数の決め方には任意性があり、決定的な方法はありません。それが、今日まで様々な乱流モデルが存在し続けている理由ですが、多くのモデルでは乱流場を表現する何らかの物理量を考え、これらの輸送方程式を 連続の式 やナビエ・ストークス方程式と連立して解くことによって渦粘性係数を決定します。

このとき、乱流モデルは流れの基礎方程式に追加される輸送方程式の数に応じて、n方程式モデルという分類がなされます。例えば、代表的な乱流モデルの一つである 標準k-εモデル は、乱流エネルギー k と 乱流消失率 ε という二つの輸送方程式を解くことから、2方程式モデル と呼ばれます。

 もっと知りたい   プラントルの混合長モデル

　付加的な物理量を考えることなく、渦粘性係数を決定する乱流モデルを 0方程式モデル といい、その一つに プラントルの混合長モデル があります。このモデルでは 乱流 における速度変動が流体粒子の移動距離 l とその間の平均速度の勾配に比例すると考え、速度変動を以下の式で与えます。

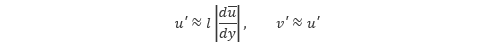
この式を用いるとレイノルズ応力は以下のように表されます。

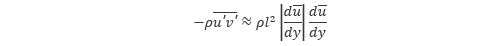
上式に絶対値記号がついているのは 応力 と速度勾配の符号を揃えるためです。また、式中の l を 混合距離 もしくは 混合長 といいます。これに対して、層流 の粘性応力は以下の式で表されます。

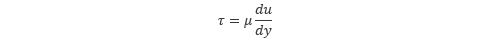
これらの式を比較すると、渦粘性係数は以下の形で表現することができます。

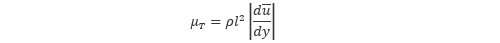
このモデルでは混合距離 l を与えられれば、付加的な計算を行うことなく渦粘性係数を決定できますが、混合距離の値は経験則によるところが大きく、その値を決めることは容易ではありません。そのため、このモデルが実用計算で用いられることはほとんどありません。一方で、プラントルの混合長モデルは、乱流の速度分布を説明する上で非常に重要な役割を果たしています。その内容については次回ご紹介します。

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。執筆したコラムに「流体解析の基礎講座」がある。　 　

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください