7.3.2 ラージエディシミュレーション (2)

　今回は サブグリッドスケール の 渦 が及ぼす影響が LES でどのようにモデル化されるかを見ていきましょう。グリッドスケール の 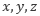方向の 流速 をそれぞれ 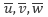とすると、フィルターを掛けた 連続の式 と ナビエ・ストークス方程式 は以下のようになります。

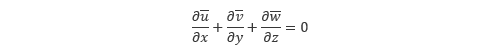
7.3.1節 で示した 基礎方程式 と比較すると、各変数がグリッドスケールの変数に変化したことを除いてよく似た形をしていますが、RANS とは異なり 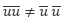などとなるため、赤字で示した付加項の表現が異なる点に注目してください。

これらはサブグリッドスケールの渦が流れに及ぼす影響を示したもので、サブグリッドスケール応力（SGS応力）と呼ばれます。そのイメージを示したものが図7.20です。SGS応力もRANSの レイノルズ応力 と同様の理由でそのまま計算することはできないため、こちらも既知の変数を用いた近似によって表現する必要があります。

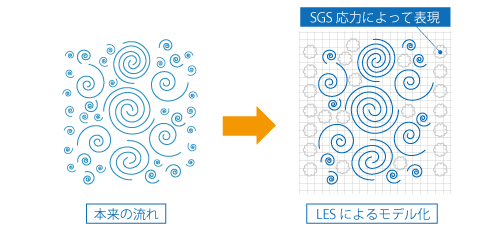
図7.20　サブグリッドスケール応力のイメージ

　SGS応力の近似に用いられるものが サブグリッドスケールモデル（SGSモデル）です。SGSモデルにはいくつかのモデルがありますが、先駆的なモデルとして スマゴリンスキーモデル が知られています。このモデルはRANSのモデル化と同じ発想で、分子粘性による 粘性応力 との類推から、SGS応力をグリッドスケール速度の勾配の大きさに比例すると考えた 渦粘性モデル で、このときの比例係数を サブグリッドスケール渦粘性係数（SGS渦粘性係数）といいます。RANSと異なるのは 乱流エネルギー などのような付加的な物理量は考えずに、メッシュサイズとグリッドスケール速度の勾配を用いて以下の式よりSGS渦粘性係数を算出する点です。

SGS渦粘性係数 = C_S・(流体の密度)・(メッシュサイズ)²・(GS速度勾配の大きさ)

上式に含まれる C_s は スマゴリンスキー定数 と呼ばれるモデル定数です。この定数は、0.1 ～ 0.2程度の範囲の値を取ることが知られていますが、適切な値が流れ場によって異なるため、普遍性を損ねる一因ともなっています。この問題に対して、流れ場の状況に応じて動的に C_s を決定する方法も提案されており、これを ダイナミックスマゴリンスキーモデル（Dynamic Smagorinsky Model, DSM）といいます。

　RANSは、時間平均に基づいて乱れの影響を等方的な渦粘性モデルによって表現するため、非定常性の強い変動が大きな影響を及ぼす流れや非等方性が強い流れを苦手とする傾向があります。これに対して、LESではより普遍的なモデル化がなされているため、RANSが苦手とする問題に対しても妥当な解が得られやすいという特徴があります。

　今回でLESに関する説明は終わりとなりますが、LESについては技術コラム「パッと知りたい！人と差がつく乱流と乱流モデル講座」でも詳しく説明していますので、こちらも併せてご覧ください。

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。執筆したコラムに「流体解析の基礎講座」がある。　 　

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください