7.3 乱流モデル

　前回、基礎方程式 をそのまま計算する DNS では、乱流 の実用計算が難しいことを説明しました。加えて、あらゆる乱れの挙動を知る必要があるケースは稀で、平均的な 流れ やその流れに影響を及ぼす大きな 渦 の挙動が分かれば十分である場合も少なくありません。

そこで、図7.5に示すように、粗い メッシュ で計算を行う代わりに、メッシュで解像できない小さなスケールの乱れの影響を何らかの物理モデルによって表現することが考えられます。このモデルのことを広義の 乱流モデル といい、代表的なモデルに レイノルズ平均モデル（RANS）や ラージエディシミュレーション（LES）などがあります。

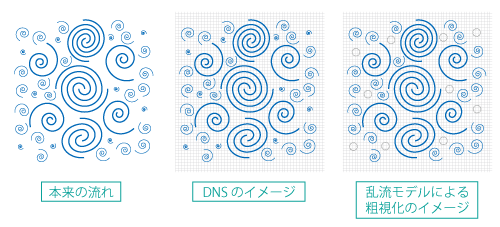
図7.5　乱流モデルの概要

7.3.1 レイノルズ平均モデル (1)

　乱流のモデル化を考えるときに、方針の一つは 非定常 である 乱流 現象の時間平均に着目して、その 定常状態 を求めるというものです。具体的には、図7.6に示すように 流速 を時間平均と変動量に分け、平均化操作を行います。これを レイノルズ平均 といいます。

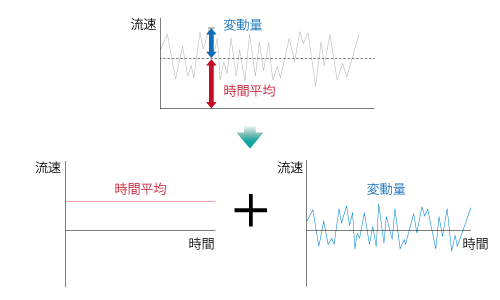
図7.6　時間平均と変動量

　レイノルズ平均を取った ナビエ・ストークス方程式 に基づく乱流解析手法を総称して レイノルズ平均モデル、またはその英語表現（Reynolds Avaraged Navier-Stokes）の頭文字を取って RANS といいます。

RANSでは時間平均を考えているため、大きさに関係なくすべての乱れがモデル化されます。このことは、計算に使用するメッシュのサイズを乱れのスケールとは独立して決定できることを意味します。

　さて、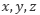方向の流速の時間平均をそれぞれ 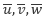, 変動量をそれぞれ 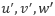, 圧力 の時間平均を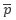とすると、レイノルズ平均に基づく 連続の式 とナビエ・ストークス方程式は以下のように表されます。

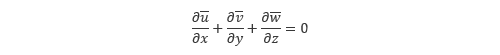
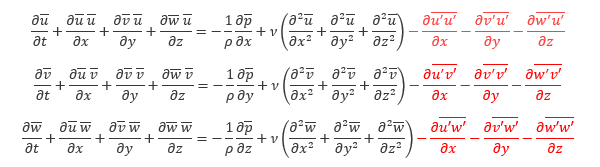
各変数が時間平均に変化したことを除いて、7.1節 で示した 基礎方程式 とよく似た形になりますが、異なるのが赤字で示した レイノルズ応力 と呼ばれる項です。この項は乱れの変動成分が流れに及ぼす影響を示したものですが、その取り扱いについては次回説明したいと思います。

 もっと知りたい   レイノルズ平均モデルの基礎方程式の導出

　レイノルズ平均モデルの基礎方程式は速度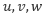を を時間平均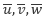 と変動値 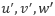を用いて、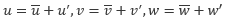 と書き換え、式全体の時間平均を取ることによって得られます。このとき、各項には以下の関係が成立するものとします。

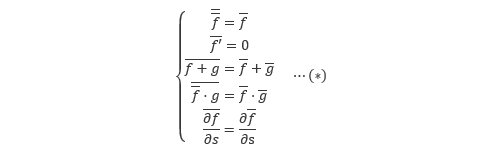
この関係が成り立つ平均化操作がレイノルズ平均と呼ばれます。まずは連続の式を見ていきます。元の連続の式を時間平均と変動量に用いた表現に書き換えます。

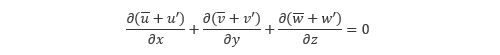
式全体の時間平均を取り、(*) の3 ～ 5番目の式を用いて整理すると以下の式が得られます。

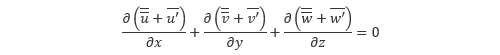
さらに (*) の1 ～ 2番目の関係式を用いることによって以下のように書き換えられます。

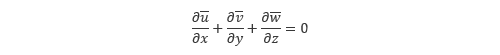
これがレイノルズ平均に基づく連続の式となります。次にナビエ・ストークス方程式を見ていきます。ここでは紙面の都合でX方向のみを例に取ると、式全体の時間平均を取り、同じく (*) の3 ～ 5番目の関係式を用いて整理することによって以下の式が得られます。

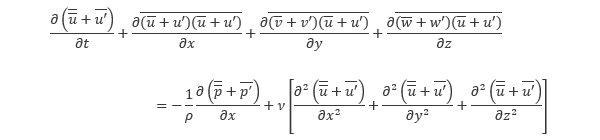
上式の移流項は以下のように書き換えられます。

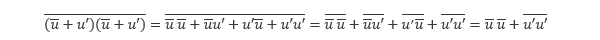
ここで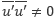であることに注意してください。これを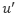と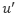に 相関 があるといいます。その他の項については、(*) の1 ～ 2番目の関係式を用いることで以下の式が得られます。

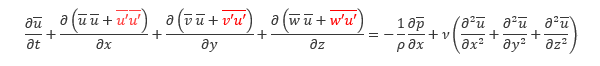
赤字で示した部分がレイノルズ応力です。これらを右辺に移項することで、前述のレイノルズ平均に基づくナビエ・ストークス方程式を得ることができます。  

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。執筆したコラムに「流体解析の基礎講座」がある。　 　

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください