7.1 乱流の性質

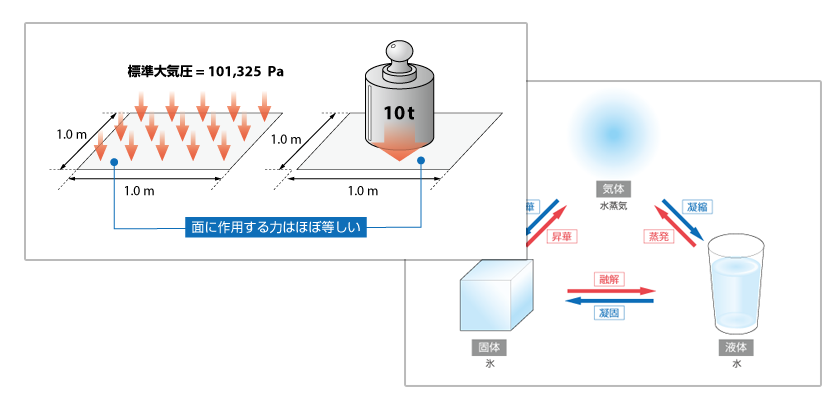
　乱流 の正確な定義を示すことは容易ではありませんが、大きな特徴を挙げれば「空間的かつ時間的に不規則な変動をする流れ」ということになります。まずは、乱流がどのようにして生じるのかを考えるために 流れ の 基礎方程式 である ナビエ・ストークス方程式 を見ていきます。

これらの方程式を 代表速度 U と 代表長さ L を用いて

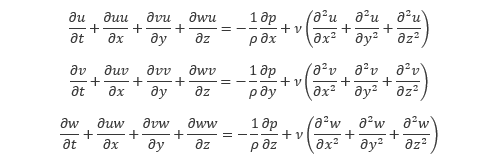
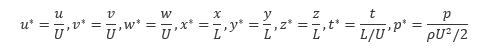
のように無次元化すると、ナビエ・ストークス方程式は レイノルズ数 Re を用いて以下のように書き換えることができます。

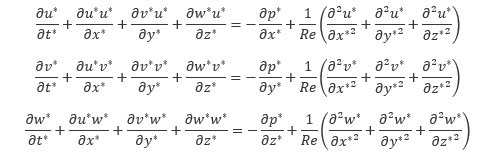
　ナビエ・ストークス方程式では慣性力と粘性力の寄与がそれぞれ 移流項 と 粘性項 によって表されますが、式を見ると移流項と粘性項の大きさの比率が1 : 1/ Reとなっており、レイノルズ数が大きくなるほど相対的に移流項（慣性力）の影響が増すことが分かります。

　慣性力の影響が大きくなれば流れの非線形性が増すため、わずかな乱れをきっかけにして流れは不規則で乱れた流れ「乱流」へと変化しやすくなります。ここでいう「わずかな乱れ」とは、流れが物体に衝突するなどの理由によって生じた 速度 のバラつきのことです。一方で、粘性力の影響が大きい場合には、流れは 粘性 の作用によって規則的で整った流れ「層流」となります。これらの違いを示したものが図7.1です。

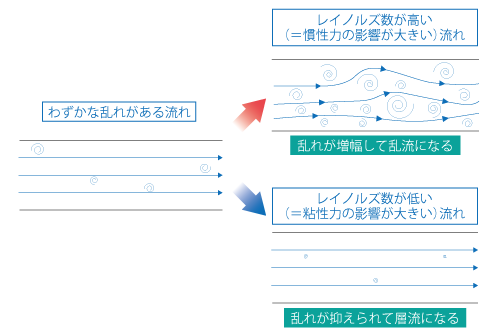
図7.1　レイノルズ数による違い

　ところで、乱流中に存在する乱れは一定ではなく、大小さまざまなスケールのものが含まれています。これはナビエ・ストークス方程式の移流項が有する非線形性の働きによって、大きなスケールの乱れがより小さなスケールの乱れへと変化していくためです。これを エネルギーカスケード といいます。

ただし、際限なく小さなスケールの乱れが生成されるわけではなく、小さなスケールの渦は粘性の影響で最終的には 熱 へと変化して消滅するため、その直前のスケールが乱れの最小スケールとなります。これを コルモゴロフ長 や コルモゴロフの長さスケール といいますが、単に コルモゴロフスケール と呼ぶ場合もあります。乱れを模式的に 渦 で表現すると、エネルギーカスケードとコルモゴロフスケールは図7.2に示すようになります。

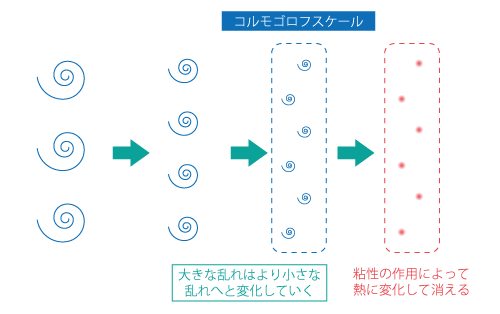
図7.2　エネルギーカスケードとコルモゴロフスケール

 もっと知りたい   エネルギーカスケード
渦の大きさを渦の直径の逆数に相当する波数で表現すると、大きな渦は低波数、小さな渦は高波数で表現されます。このことを用いて、非線形項の作用によって大きな渦がより小さな渦に変化する（波数が大きくなる）ことを確認してみます。1次元の流れを考え、その乱流の変動が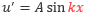で表されるとします。この変動が移流項に作用すると以下のようになります。

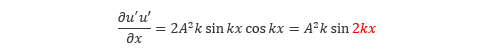
　元の変動と比較すると、波数が2倍の変動が作り出されていることが分かります。このような過程を繰り返すことによって、大きな渦は小さな渦へと変化していくため、流れ場には様々なスケールの乱れが混在することになります。

 もっと知りたい   コルモゴロフのマイクロスケール
　最小スケールの渦の運動は最小スケールの渦が受け取るエネルギー、すなわち大きなスケールの渦が失うエネルギーと最小スケールの渦から粘性によって失われるエネルギーによって決まると考えられます。そこで、単位質量あたりの エネルギー散逸率 ε [m²/s³] と 動粘性係数 ν [m²/s] を用いて、最小スケールの渦に対する長さ・時間・速度のスケールを次元解析的に構成すると以下のようになります。

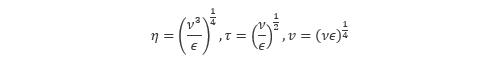
　これらを コルモゴロフのマイクロスケール といいます。このうち、長さのスケールが最小の渦のサイズを表しており、前述のコルモゴロフスケールに対応しています。さて、これらのスケールを用いてレイノルズ数を構成すると以下のようになります。

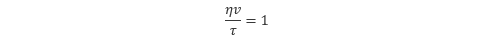
　高レイノルズ数の乱流では、マクロな視点に立てば慣性力が支配的となることから、粘性の働きはさほど重要ではないように思えます。しかし、上記のレイノルズ数が1となることからも想像できるように、最小スケールの乱れに対しては粘性が非常に大きな影響を及ぼします。最終的には乱れが粘性によって散逸するように、乱流の場合でも粘性の影響を無視することはできません。

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。執筆したコラムに「流体解析の基礎講座」がある。　 　

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください