7.3.1 レイノルズ平均モデル (3)

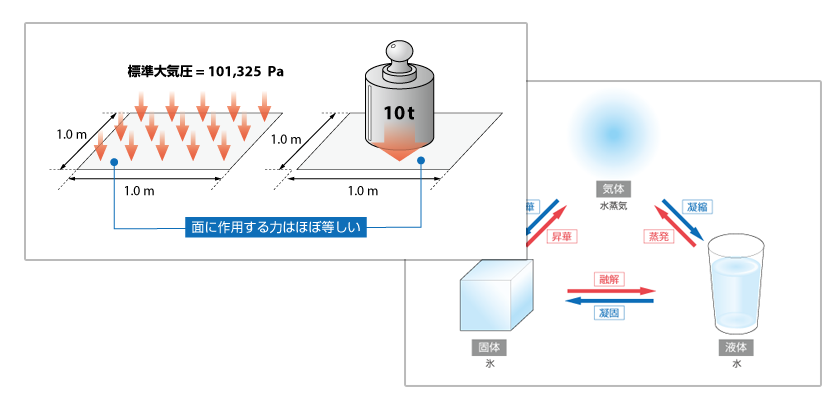
　前回と前々回で RANS の 基礎方程式 を見てきましたが、これらは等方性の高レイノルズ数流れを前提としたものです。この等方性とは、特定の方向性を持たず、観測している座標系の回転や変換などによって統計量が変化しない性質で、乱流境界層 でこの性質を満たすのは、壁から少し離れた 乱流層 となります。

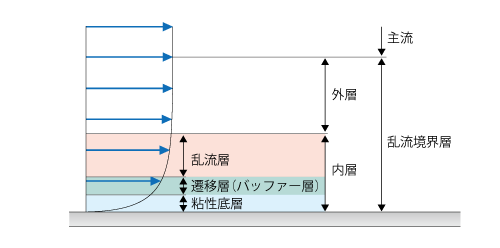
図7.9　乱流境界層の構造

　一方、壁面近傍は 粘性 の影響が大きく、非等方性が強く現れる領域です。したがって、等方性の高レイノルズ数流れを前提としたRANSの基礎方程式を壁面近傍にもそのまま適用することはできず、何らかの工夫が必要となります。その方法によって、RANSの 乱流モデル は 高レイノルズ数型モデル と 低レイノルズ数型モデル に大別されますが、今回はこのうち高レイノルズ数型モデルについて説明します。

　高レイノルズ数型モデルとは、モデルが適用できない壁面近傍は計算しない代わりに、その部分の情報を 境界条件 で補って計算を行うモデルで、代表的なモデルとして 標準k-εモデル が知られています。境界条件には乱流境界層の速度分布が用いられ、一般にこれを 壁法則 といいます（速度分布の具体的な式は 3.5.2節 の  もっと知りたい をご覧ください）。

　メッシュについては、壁面から一番目の計算点を 対数則 が成立する乱流層、すなわちy⁺ = 30 ～ 1,000程度の範囲に配置します。前述のように壁面と壁面から一番目の計算点との間は境界条件によって考慮され、計算は行われません。それを示したものが図7.10です。

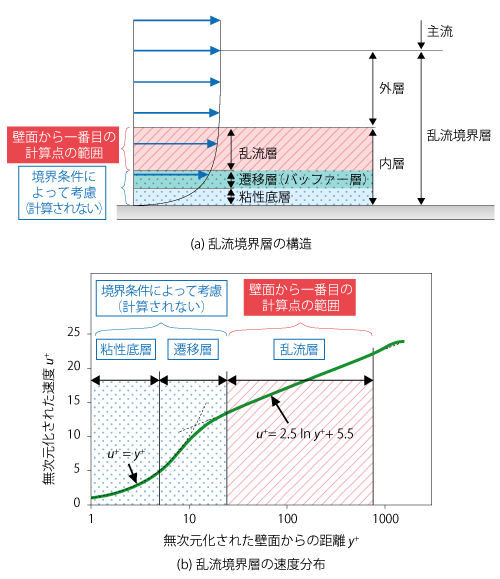
図7.10　高レイノルズ数型モデルにおける壁面近傍の取り扱い

　高レイノルズ数型モデルでは、物理量の勾配が最も急になる壁面近傍を解像しなくてもよいため、比較的粗いメッシュで計算を行える利点があります。通常は、メッシュ が細かいほど計算の精度面で有利となることが多いですが、高レイノルズ数型モデルに限っては、メッシュを細かくし過ぎて 粘性底層 や 遷移層 に計算点が配置されてしまうと、逆に精度を悪化させてしまうため、壁から少し離れたy⁺ > 30に配置することが重要です。

　一方で、境界条件に用いられている対数則は壁面に沿う乱流境界層で成り立つもので、あらゆる流れに対して普遍的に成立するわけではありません。そのため、大きな 剥離 を伴わない流れに対しては良好な結果を与えますが、壁法則から逸脱した流れに対しては、境界条件に起因する差異を生じやすいことに注意が必要です。

 もっと知りたい   乱流層の速度分布（対数則）

　乱流 は不規則な変動を伴う 流れ であり、その速度分布を理論的に解析することはできませんが、実験に基づいた解析から特定の状況における平均速度の分布が知られています。

　まず、壁面近くの乱流運動は壁面に拘束されるため、混合距離 l は壁面からの距離 y に比例すると考えられることから、比例係数を κ として、 l ＝ Ky とおきます。これを プラントルの混合距離の仮説 といいます。また、乱流によって壁面に作用する 応力 は レイノルズ応力 >> 粘性応力 と考えられることから、壁面せん断応力 ≈ レイノルズ応力 とおくことができます。したがって、壁面せん断応力 τ_w は、前回の  もっと知りたい で示したレイノルズ応力を用いて以下のように表わされます。

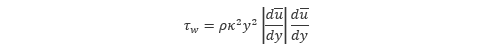
式中の絶対値はせん断応力の符号との整合を考慮するためのものです。ここで 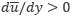として、次の式で定義される 摩擦速度 u_*

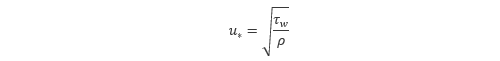
を用いて τ_w を消去すると、以下の式が得られます。

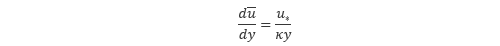
この式を y について積分すると

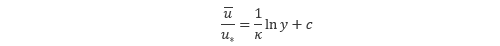
となり、対数則の式が得られます。また、流速と壁からの距離を無次元化した以下の表現も多く用いられます。

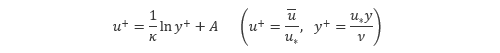
なお、κ のことを カルマン定数 といい、滑らかな面においては実験的に κ ＝ 0.4, A = 5.5 となることが知られています。また、プラントルの仮説では壁面近くを仮定しているものの、この式は壁面のごく近傍では成り立たず、壁から少し離れた乱流層で成立することに注意してください。

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。執筆したコラムに「流体解析の基礎講座」がある。　 　

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください