船のCFD 9. 自航要素の推定(2)

9. 自航要素の推定(2)
自航状態の船体周りの流れをCFDにより計算する方法は、船体周りの流れとプロペラ周りの流れの両方をCFDで解くやり方と、船体周りの流れだけをCFDで解き、プロペラの影響はナビエストーク方程式に体積力として加える方法の2つに分けられます。前回述べたように前者の方法は計算負荷が大きいので、それに代わる方法として後者の方法が研究されてきました。後者の方法では、プロペラの影響を表す体積力はプロペラモデルを用いて計算します。プロペラモデルには、指定した推力をあらかじめ決めた形状の範囲に分布させるモデルや、プロペラの位置の速度分布を使って翼素運動量理論やポテンシャル近似に基づく理論計算によって力の分布を求めるモデルなど、様々なモデルが存在します。
ここでは、「簡易プロペラモデル」[1]を用いて、ばら積み船の自航状態の計算を行った例を紹介します。簡易プロペラモデルはプロペラを無限の翼数を持つ薄いディスクとして近似するモデルで、流入する流れに応じた推力およびトルクと流体力の分布が得られるモデルです。プロペラによる流体力は翼が通過するたびに変化しますが、このモデルではプロペラ面における時間平均の力の分布が得られるので、定常計算を行うことができることが利点です。
|
|
|
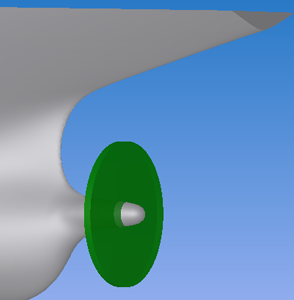
船型は第4回「船体抵抗の推定(2)」でも登場したばら積み船JBC(Japan Bulk Carrier)です。計算は水槽試験と同じ舵無しの状態で行いました。模型の船長 L は7m、速度 U は1.179m/s、レイノルズ数 Re = UL/ν(νは水の動粘性係数)は7.46×106です。計算領域を下の図に示します。自由表面は対称面としました。船体形状は左右対称なのですが、一軸船ではプロペラの回転によって流れが左右非対称になるので、左右両舷を計算する必要があります。SST k-ωモデルを用いた定常RANS解析を行います。メッシュのセル数は約2,200万、節点数は約660万で、y+の値は0.2としました。

自航する船体周り流れの計算領域
計算は簡易プロペラモデルをオフにした曳航状態と、簡易プロペラモデルを用いた自航状態の両方について行います。自航状態のプロペラ回転数は実験の自航点と同じ7.8rpsとしました。自航試験では通常、船体の抵抗と推力がちょうど釣り合うように回転数を調整しますが、今回の計算ではその過程を省略しています。
曳航状態と自航状態の全抵抗係数を実験[2]と比較したグラフを以下に示します。船の全抵抗係数 Ct は、抵抗値を R、水の密度を ρ、船速を U、浸水表面積を S として、
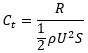
と定義されます。グラフから、自航状態では曳航状態より抵抗が1割強くらい増加することが確認出来ます。
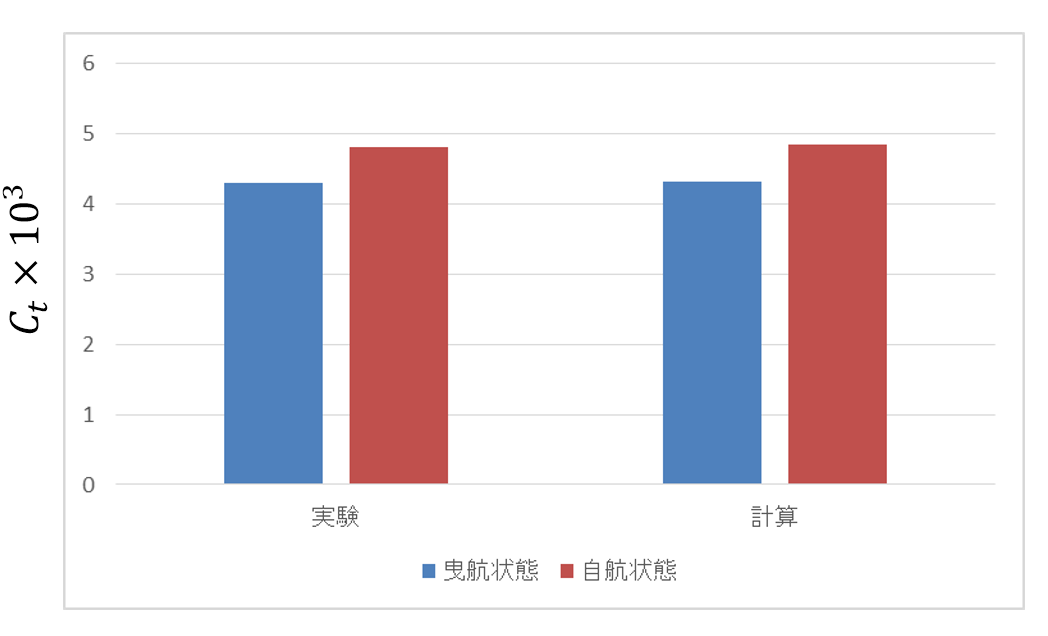
曳航状態と自航状態の全抵抗係数の比較
計算で得られたプロペラの推力係数 KT とトルク係数 KQ を実験と比べた表を以下に示します。
| 実験 | 計算 | |
| Kr | 0.217 | 0.227 |
| 10×KQ | 0.279 | 0.283 |
なお、推力係数 KT とトルク係数 KQ は、推力を T、トルクをQ、回転数をn、プロペラ直径をDとして、
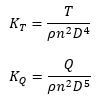
と定義されます。
自航要素は推力減少率 t、伴流率 w、プロペラ船後効率比 ηR という3つの数字で表されます。推力減少率 t はプロペラの影響による船体の抵抗増加を表し、曳航状態と自航状態の抵抗の差を∆R、推力を T として以下の計算で求められます。
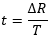
伴流率 w は船体の影響によってプロペラに流入する流れが遅くなる効果を表します。自航状態では、プロペラは不均一な船体の伴流中で作動しているので、一様流中の場合と異なりプロペラに流入する流れの流速を直接計測することが出来ません。一方、推力とトルクの値は直接計測することができるので、プロペラ単独性能曲線を使って、計測した推力からプロペラ前進速度 VA を逆に求めます。求めたプロペラ前進速度 VA と船速 V から、伴流率 w は
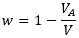
として求められます。なお、推力からプロペラ前進速度を逆算するこのやり方を、推力一致法と呼んでいます。
プロペラ船後効率比 ηR は伴流中でのプロペラ効率の変化を表わし、一様流中でのプロペラ効率を ηo として以下の計算で求められます。
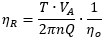
計算から求めた自航要素を実験と比較した表を以下に示します。簡易プロペラモデルを用いた計算でも自航要素をある程度の精度で求めることが出来ることが分かります。
| 実験 | 計算 | |
| 推力減少率t | 0.198 | 0.194 |
| 伴流率w | 0.589 | 0.619 |
| プロペラ船後効率比ηR | 1.014 | 1.020 |
曳航状態と自航状態のプロペラ面を通過する流線と下流側の断面の流速分布を以下に示します。自航状態ではプロペラにより流れが加速されて、船体周りの流れも曳航状態とは異なることが確認出来ます。
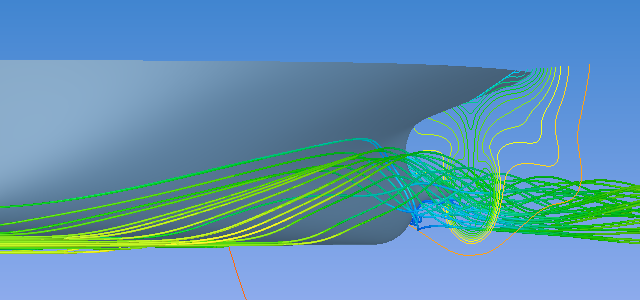
曳航状態
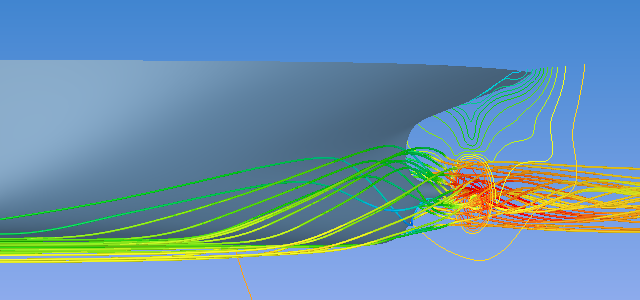
自航状態
参考文献
[1] 中武一明, 船体とプロペラの相互干渉について, 西部造船会会報, 第34巻, 1967
[2] Proceedings of Tokyo 2015, A Workshop on CFD in Ship Hydrodynamics (2015), Tokyo, Japan

著者プロフィール
川村 隆文 | 1970年 東京生まれ
1993年 東京大学工学部船舶海洋工学科卒業
1995年 東京大学大学院工学系研究科船舶海洋工学専攻修士課程修了
1998年 博士(工学)の学位を取得
デンマーク国際数値流体力学研究所(ICCH)研究員、運輸省船舶技術研究所研究官、東京大学大学院工学系研究科講師、東京大学大学院工学系研究科准教授などを経て2010年から株式会社数値流体力学コンサルティングの代表を勤める。専門は数値流体力学、船舶流体力学、プロペラなどの流体機械、キャビテーションなど。
最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください