10. 自航要素の推定（３）

前回はプロペラを簡略化したプロペラ体積力モデルを用いて自航状態の船体周りの流れを計算した例を紹介しました。船体の自航要素を求める目的であれば、プロペラ体積力モデルを用いる方法が適していることが多いですが、船体とプロペラの相互干渉についてより詳細な情報が必要になる場合にプロペラについてもCFDで直接計算する方法が採られます。

プロペラと船体の相互干渉には定常成分と時間変動成分の両方があります。燃費に直接関係するのは定常成分ですが、次回以降解説するプロペラのキャビテーションでは時間変動成分が本質的に重要になります。また、自航要素は主に船体の形状によって決まりますが、プロペラ形状にも依存します。プロペラ体積力モデルはプロペラを簡略化して取り扱うので、自航要素も考慮してプロペラ設計を検討するというような用途には不向きです。

さらに最近ではプロペラの前や後にダクトやフィンなどの省エネ付加物が設置される例が増えています。省エネ付加物の多くは自航要素を改善することが狙いですので、自航状態で評価を行う必要がありますが、これらの付加物は寸法的にプロペラと同程度かそれより小さいため、CFD解析でプロペラを簡略化してしまうと、正しい評価を行えない可能性があります。

船体付加物の例（Eco-Stator：流体テクノ株式会社提供）

プロペラをCFDで直接計算する場合、プロペラ周りのメッシュをプロペラと一緒に回転移動させる方法を使うのが一般的です。具体的には、プロペラを囲う円筒状の領域を回転領域として、その外側の静止領域に分けて計算を行います。このとき、静止領域と回転領域の接合面はメッシュが不連続になるので、不連続接合（又は、スライディングメッシュ法と呼ぶこともあります）という機能を用いることで領域をまたいで連続な解が得られるようにします。

プロペラ周りの回転領域のメッシュ

前回紹介した自航状態のJBCについて、簡易プロペラモデルを用いて計算した場合と、プロペラを直接計算した場合で中心断面上の圧力分布を比較して見ました。プロペラを直接計算した場合にはプロペラ翼端から渦が発生している様子なども捉えられていますが、簡易プロペラモデルを用いた計算ではプロペラによる流れが簡略化され定常成分だけになっている様子がよく分かります。

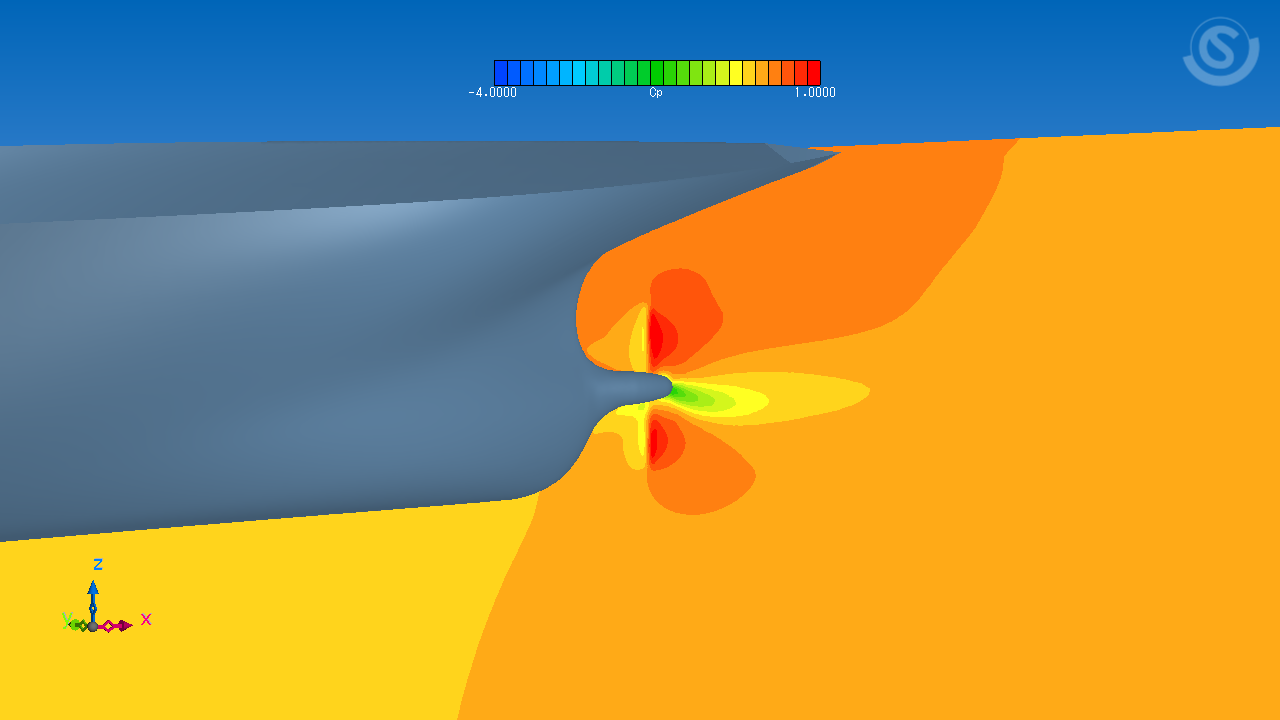
中心断面の圧力分布（簡易プロペラモデルを用いた計算）

中心断面の圧力分布（プロペラを直接計算）

プロペラ翼に流入する流れの速さは位置によって異なり、翼に作用する流体力や表面の圧力分布は一回転する間に周期的に変化します。プロペラ翼には繰り返し荷重が掛かるので疲労破壊の可能性を考慮して十分な強度とする必要があります。また、圧力が変動することによりキャビテーションが発生します。このような非定常現象を取り扱うためには、プロペラ周りの流れもCFDで直接計算する必要があると言えます。

プロペラ表面の圧力分

著者プロフィール
川村 隆文 | 1970年 東京生まれ
1993年 東京大学工学部船舶海洋工学科卒業
1995年 東京大学大学院工学系研究科船舶海洋工学専攻修士課程修了
1998年 博士（工学）の学位を取得

デンマーク国際数値流体力学研究所（ICCH）研究員、運輸省船舶技術研究所研究官、東京大学大学院工学系研究科講師、東京大学大学院工学系研究科准教授などを経て2010年から株式会社数値流体力学コンサルティングの代表を勤める。専門は数値流体力学、船舶流体力学、プロペラなどの流体機械、キャビテーションなど。

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください