4. 船体抵抗の推定（２）－粘性抵抗の推定

今回は船体の二重模型周りの流れの計算の例を紹介します。対象はJBC（Japan Bulk Carrier）というばら積み船の船型です。ちなみに、ばら積み船（Bulk Carrier）の「ばら」は貨物を箱に入れないでそのまま積むということを意味しています。ばら積み船が運ぶ主な対象は鉄鉱石、石炭、穀物、木材などです。なお、貨物を運ぶ船には、ばら積み船の他に原油、石油製品、液化天然ガス（LNG）、液化プロパンガス（LPG）などの液体を運ぶタンカー、荷物を規格化されたコンテナに詰めて運ぶコンテナ船、自動車の完成品を運ぶ自動車運搬船などがあります。

JBCはCFDの検証などを目的として、海上技術安全研究所が中心となって設計した船型で、船体形状データと実験データが公開されている船型です。このように、形状と実験データが公開されている船型は数が限られており、ベンチマークデータとして貴重な存在です。

計算は水槽試験と同じ条件で行いました。模型の船長Lは7m、速度Uは1.179m/s、レイノルズ数Re=UL/ν（νは水の動粘性係数）は7.46×10⁶です。計算領域を下の図に示します。船体は左右対称なので、左半分のみを計算します。流入境界（図の右側）は流速固定、流出境界（図の左側）は圧力固定とします。船体表面はノースリップの壁面条件とし、他の境界は滑り壁としました。SST k-εモデルを用いたRANS解析を行います。

船体の二重模型周り流れの計算領域

船尾周りのメッシュを下に示します。要素数は約620万、節点数は約180万です。船体の周りに境界層メッシュが挿入されていることが確認出来ると思います。船の抵抗は摩擦抵抗が大きな割合を占めており、摩擦抵抗を正確に予測するためには、適切な境界層メッシュを作成することがとても重要です。

船尾周りの計算メッシュ

境界層メッシュのパラメータは第一層高さ∆yと、成長率r、層数nです。第一層高さについては、∆yを壁面せん断応力で無次元化した値であるy⁺を指標として値を決めます。y⁺の定義は以下の通りです。

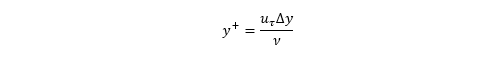
uτは摩擦速度で、

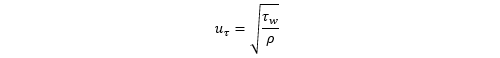
と定義されます。ρは流体密度で、τwは壁面せん断応力です。壁面せん断応力は場所によって異なるのでy⁺の値も場所によって異なることになりますが、平均値に対するy⁺の値が目安としてよく用いられます。適切なy⁺の値は使用する乱流モデルに依存し、低レイノルズ数型モデルでは1以下の値、標準k-εモデルなどの高レイノルズ数型のモデルでは30以上の値が一般に推奨されます。ここでは、低レイノルズ数型のモデルであるSST k-εモデルを使っているので、y⁺の値が0.1になるようにΔyの値を設定することにします。船体の周りの壁面せん断応力は計算するまで分からないので、代わりに平板の経験式などを用いて見積もります。例えばシェーンヘルの式、

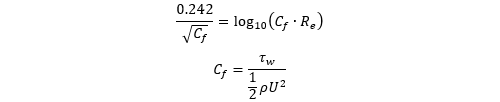
を使うと、Re=7.46×10⁶のときの摩擦抵抗係数Cfは3.08×10^-3と求まります。これからτw、uτを順に求めてy⁺の定義式に代入すると、y⁺=0.1とするためには、Δy=2.39×10^-6mとする必要があることが分かります。成長率rは1.1～1.3くらいが適当です。ここでは1.2としました。境界層メッシュ全体の高さhは、

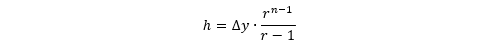
から求められるので、仮に全体の高さhをある決まった値にしたいのであれば、層数は以下の式で求めた値を整数に丸めることで求めることができます。

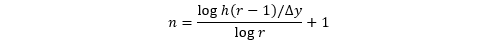
ここでは、全体の高さhが船長の約0.5%になるように層数nを決めました。Δy=2.39×10^-6、h=7×0.005、r=1.2を代入すると、n=45となります。

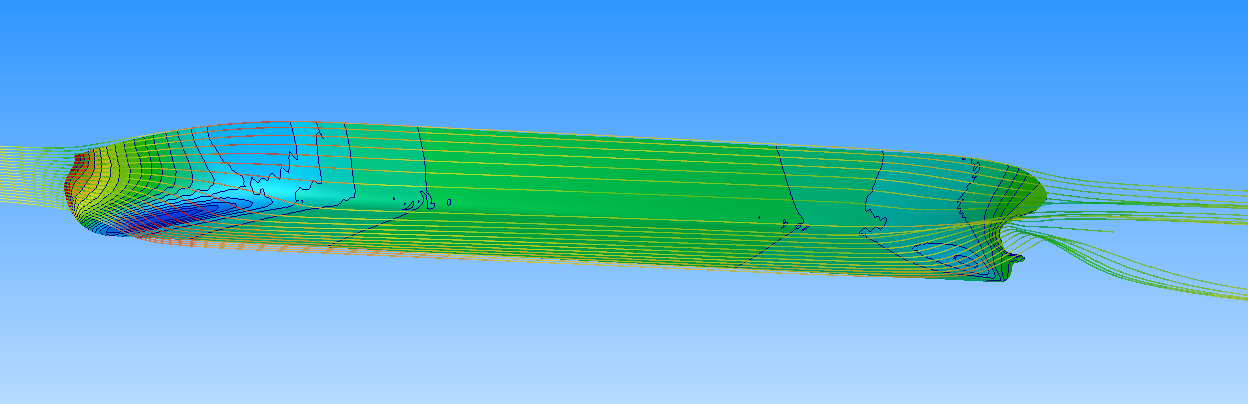
計算結果を下に示します。船尾の近くで流れが剥離し、縦渦が形成されていることが観察出来ます。プロペラは船尾の複雑な伴流の中で作動するので、抵抗を推定することに加えて、プロペラ設計のために、プロペラに流入する流れを正確に予測することも求められます。

船体周りの圧力分布と流線

船尾付近の主流方向速度の分布

粘性抵抗の計算では、抵抗の計算値がy⁺の値に敏感であることに注意する必要があります。下の図はy⁺の値を変えたメッシュを作成して計算を行い、得られた抵抗値の水槽試験結果（文献 [1] ）に対する比をプロットしたものです。水槽試験結果には造波抵抗が含まれているので、直接比較することは出来ませんが、y⁺の値が変わると抵抗の計算値は10%近くの幅で変化することが分かります。この結果はSST k-εモデルを用いた場合のものなので、違う乱流モデルでは異なった変化をします。

SST k-εモデルは低レイノルズ数型のモデルなので、y⁺の値を1以下にするというのが基本ですが、最近の実装ではy⁺の値が大きいときには壁関数が自動的に適用されるようになっています。この切り替えはy⁺=10あたりで行われ、この前後では抵抗値はy⁺の値に特に敏感になります。

以上のことから、異なる船型の抵抗値を比較する場合は、必ずy⁺の値を揃えて比較するということと、y⁺=10前後の値は避けることが重要であると言えます。

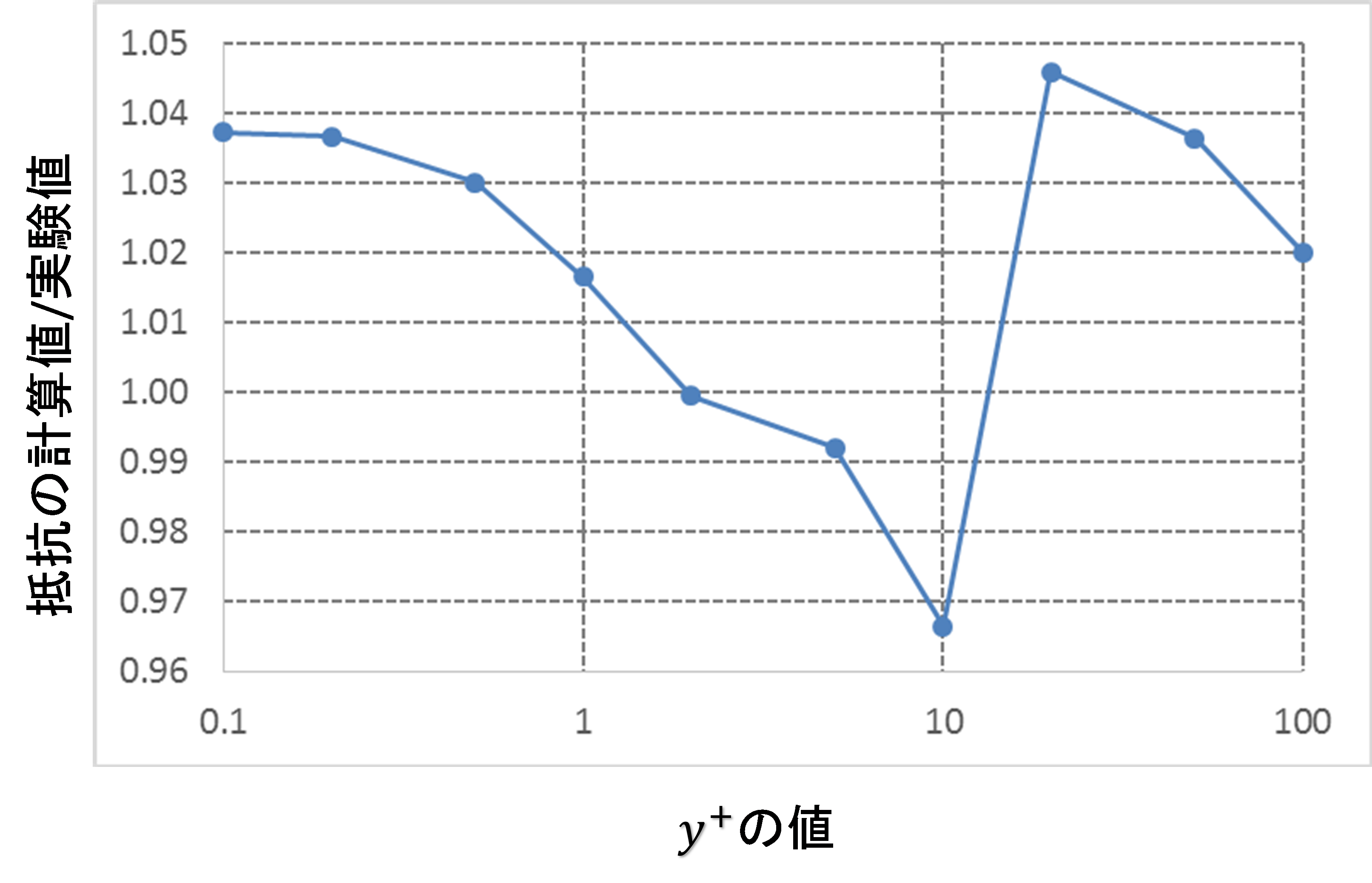
y⁺の値と抵抗の計算値の関係

参考文献
[1] Proceedings of Tokyo 2015, A Workshop on CFD in Ship Hydrodynamics (2015), Tokyo, Japan

著者プロフィール
川村 隆文 | 1970年 東京生まれ
1993年 東京大学工学部船舶海洋工学科卒業
1995年 東京大学大学院工学系研究科船舶海洋工学専攻修士課程修了
1998年 博士（工学）の学位を取得

デンマーク国際数値流体力学研究所（ICCH）研究員、運輸省船舶技術研究所研究官、東京大学大学院工学系研究科講師、東京大学大学院工学系研究科准教授などを経て2010年から株式会社数値流体力学コンサルティングの代表を勤める。専門は数値流体力学、船舶流体力学、プロペラなどの流体機械、キャビテーションなど。

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください