7.3.1 レイノルズ平均モデル (4)

　前回、RANS の 乱流モデル が 高レイノルズ数型モデル と 低レイノルズ数型モデル に大別されることを書きました。今回は低レイノルズ数型モデルについて説明していきます。

　乱流境界層 のうち、壁面に近い領域では 粘性 の影響が強く、乱れの非等方性が強く現れます。この領域における乱れの振る舞いを 壁面漸近挙動 といいますが、高レイノルズ数型モデルは漸近挙動を満たすモデル化となっていないため、壁面近傍の計算にモデルをそのまま用いることができませんでした。そこで、これを満たすように改良されたモデルが低レイノルズ数型モデルです。代表的なモデルとして、安倍・近藤・長野モデル（AKNモデル）や SST k-ω モデル などが知られています。

　低レイノルズ数型モデルでは、高レイノルズ数型モデルよりも細かい メッシュ を使用して、壁面近傍も含めた 流れ を計算します。そのため、境界条件 には 対数則 ではなく、厳密な壁面境界条件であるノースリップ（滑りなし）条件を使用します。

　メッシュは 粘性底層 の流れを解像できるように、壁面から一番目の計算点を粘性底層、すなわち y⁺ = １ 程度に配置することが理想的です。しかし、計算負荷の問題からそこまで細かいメッシュを作成できない場合には、 y⁺ < 5 程度というのが一つの目安になります。なお、低レイノルズ数型モデルは壁から離れたとしても、高レイノルズ数型モデルと同等の定式化になるため、メッシュが粗い場合にも直ちに合理性を欠くわけではなく、メッシュサイズに応じた計算がなされます。

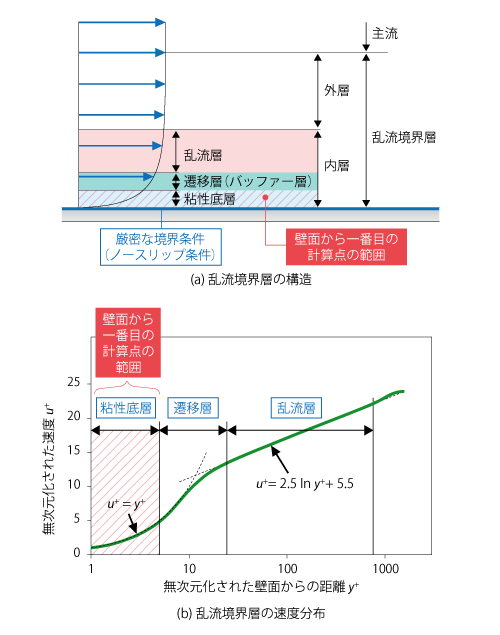
図7.11　低レイノルズ数型モデルにおける壁面近傍の取り扱い

　低レイノルズ数型モデルでは壁面近傍の流れも計算されるため、剥離 や 再付着 を伴う流れのように対数則が成立しない流れに対して、高レイノルズ数型モデルよりも妥当な解が期待できる特徴があります。一方で、解が流入乱流量の影響を受けやすい点に注意が必要です。

　なお、高レイノルズ数型モデルや低レイノルズ数型モデルという名称は、図7.12に示すように、それぞれのモデルが壁面から一番目の計算点を乱流境界層における高レイノルズ数領域（乱流層）や低レイノルズ数領域（粘性底層）に配置することに由来したものです。レイノルズ数 といえば、解析対象の 代表速度 や 代表長さ を用いて定義されるマクロな流れのレイノルズ数が思い浮かびますが、それとは異なることに注意してください。したがって、レイノルズ数が高い流れには高レイノルズ数型モデルを使わなければならないとか、レイノルズ数が低い流れには高レイノルズ数型モデルを使用できないということはありません。

　しかしながら、レイノルズ数が低い流れほど粘性底層が厚くなり、y⁺ = 1 を満たすメッシュは大きく（粗く）なることから、レイノルズ数が低い流れほど低レイノルズ数型モデルを使いやすい状況となります。

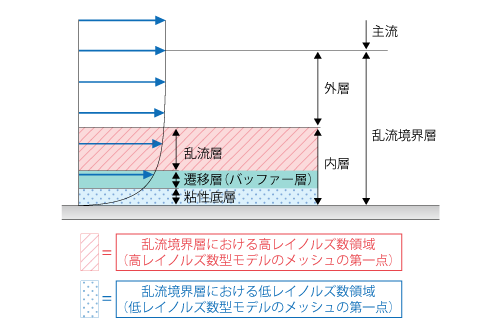
図7.12　高レイノルズ数領域と低レイノルズ数領域

　今回でRANSに関する説明は終わりとなりますが、RANSについては技術コラム「パッと知りたい！人と差がつく乱流と乱流モデル講座」でも詳しく説明していますので、こちらも併せてご覧ください。

 もっと知りたい   粘性底層の速度分布

　粘性底層においては、粘性応力 >> レイノルズ応力 となることから、壁面せん断応力 τ_w は以下の式で与えられます。

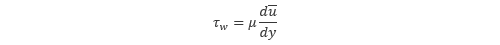
上式を積分することによって、以下の粘性底層における速度分布が得られます。

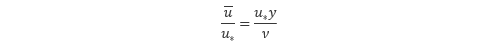
また、流速と壁からの距離を無次元化した以下の表現も多く用いられます。

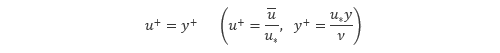
上式の速度分布を前回の  もっと知りたい  で示した対数則と併せてグラフで示すと、図7.13のようになります。

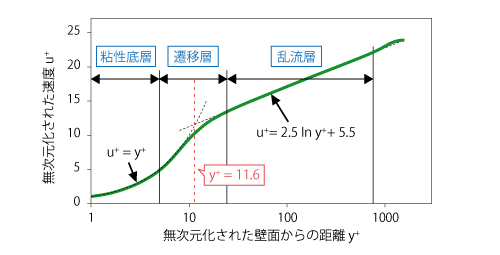
図7.13　乱流境界層の速度分布

　この図から粘性底層の速度分布と乱流層の速度分布（対数則）は y⁺ = 11.6 で交わることがわかります。しかしながら、実際には速度分布がこの値を境にして明確に切り替わるわけではなく、y⁺ = 4 付近で徐々に粘性底層の速度分布から外れて対数則に近づいていき、y⁺ = 30 付近以降で対数則に一致するという傾向を示します。

この速度分布が変化する途中の領域を 遷移層、または バッファー層 といいますが、遷移層は粘性底層や乱流層ほど定まった速度分布を持たないため、メッシュの一点目をこの付近に配置することはできるだけ避けるのが望ましいといえます。

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。執筆したコラムに「流体解析の基礎講座」がある。　 　

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください