装置設計者のための騒音の基礎 第31回
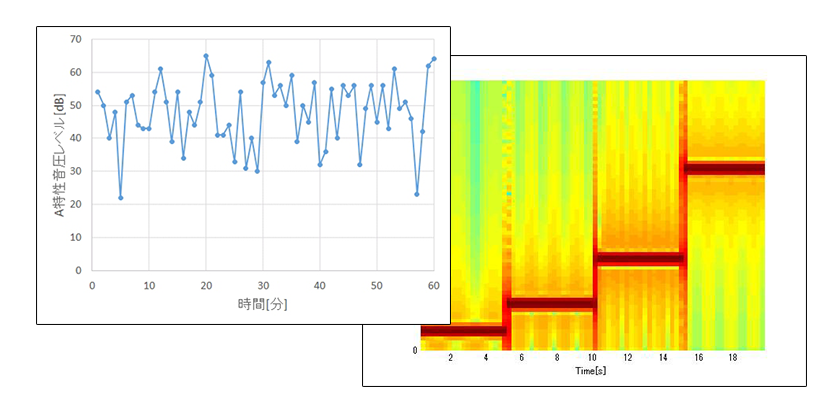
エンベロープ処理
この連載では、製品開発・設計をされる方を対象に、騒音に関する基礎的な事項を説明しています。短時間FFTは、振幅変調音の周波数と変動周期を同時に捉えることができますが、時間分解能と周波数分解能の制約があります。一方、変動周期だけわかれば良いといった問題では、今回説明するエンベロープ処理が、時間分解能と周波数分解能の制約もなく、便利です。
エンベロープ処理は、包絡線処理とも呼ばれ、振幅の外形を取り出す処理です。図1が10Hzで振幅変調した波形で、図2がエンベロープ処理を行った後の波形です。10Hzで変動する振幅の変化が取り出せていることがわかります。図2の波形にFFT処理を行うと、変動の周波数スペクトルが得られます。
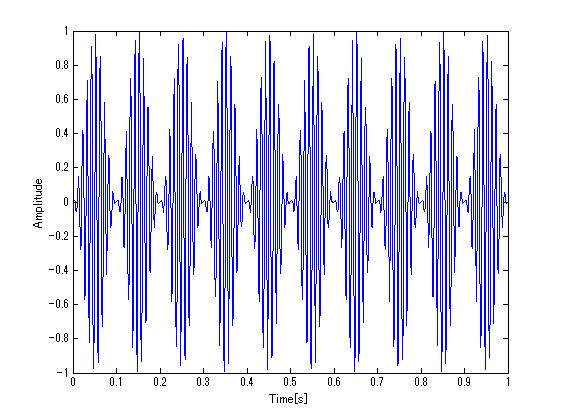
図1 10Hzの振幅変調波形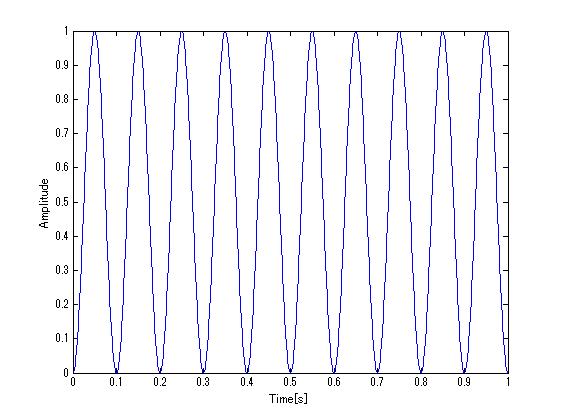
図2 エンベロープ処理結果
エンベロープ処理は、信号にヒルベルト変換を施すことで得られます。ヒルベルト変換とは、下記に示す変換で、信号x(t)の周波数スペクトルを、ナイキスト周波数(標本化周波数の1/2)未満では、位相を90度遅らせる、また、ナイキスト周波数超えでは、位相を90度進めるという操作を行った後、フーリエ逆変換を行います。(1)式において、Fはフーリエ変換、F-1 はフーリエ逆変換で、jは虚数単位を示します。
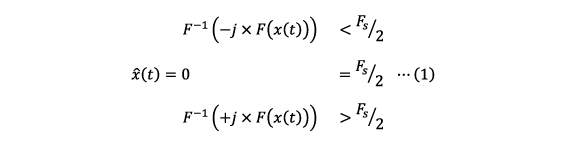
エクセルでエンベロープ処理を行ってみます。図3に示すように、A列に0から1/1024ずつ増加する値を生成し、時間軸とします。B列には、0から1ずつ増加する値を生成し、周波数軸とします。C列に100Hzの搬送波を2Hzで変調した信号を用意します。D列にFFT処理結果を出力します。E列にFFT処理結果の絶対値を取り出し、2/データ数をかけると、周波数スペクトルが得られます。図4が周波数スペクトルで、100Hzの搬送波周波数を中心として左右に98Hzと102Hzの側帯波が見られます。次に、F4からF515までは"=COMPLEX(IMAGINARY(D),-IMREAL(D))"と入力し、F516は0で、F517からF1027までは"=COMPLEX(-IMAGINARY(D),IMREAL(D))"と入力します。G列に逆FFT処理結果を出力し、H列に絶対値を取り出すと、エンベロープ処理結果が得られます。I列にH列のFFT処理結果を出力し、J列にFFT処理結果の絶対値を取り出し、2/データ数をかけると、エンベロープ処理後の周波数スペクトルが得られます。図5がエンベロープ処理後の周波数スペクトルで、変調周波数2Hzが観測されます。
ただし、エクセルのFFT処理は精度が良くないため、エンベロープ処理後の波形に搬送波の影響が出ます。以上の説明は、エンベロープ処理を理解するためであり、実際の処理には、FFTアナライザの機能あるいは、MATLABなどを使われることをお勧めします。なお、図1と図2はMATLABを使って計算しました。

図3 エクセルシートへの数式の入力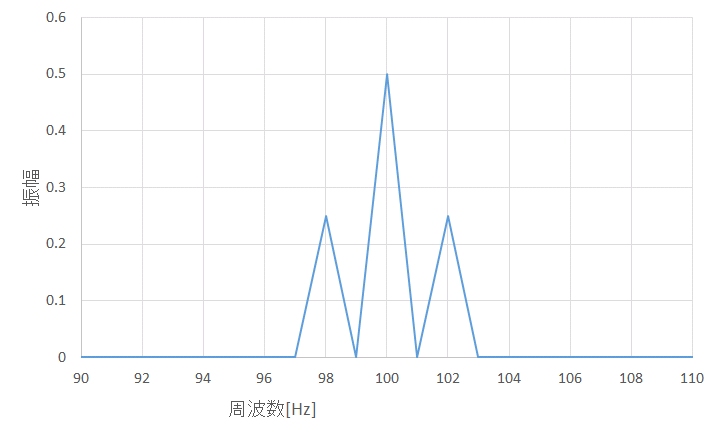
図4 信号波形の周波数スペクトル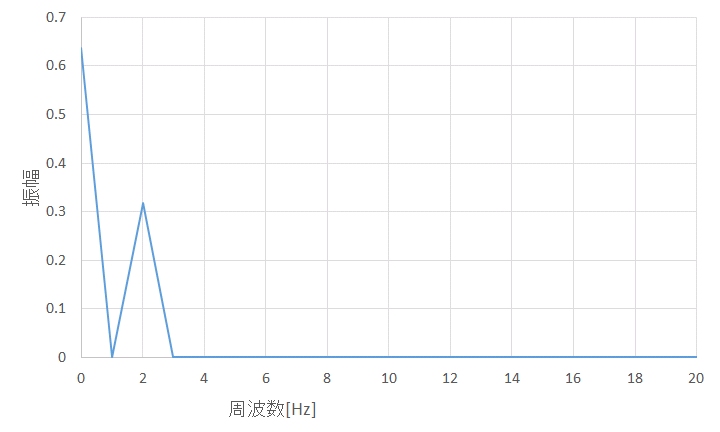
図5 エンベロープ処理後の波形の周波数スペクトル
次回は、エンベロープ処理の例として、軸受振動の解析について説明します。
【参考文献】 機械音響工学 鈴木ほか コロナ社

著者プロフィール
御法川 学 氏 | 法政大学 理工学部 機械工学科 教授
環境計量士(騒音・振動)
1992年 法政大学大学院 工学研究科 機械工学専攻
1992年 株式会社荏原総合研究所 入社
1999年 法政大学工学部 助手
2001年 東京工業大学にて学位取得、博士(工学)
2004年 法政大学工学部 助教授
2010年 法政大学理工学部 教授

著者プロフィール
伊藤 孝宏 氏 | オリエンタルモーター株式会社 技術支援部主席研究員
1982年 筑波大学基礎工学類卒業。新日本製鉄株式会社に入社、加熱・冷却設備の開発に従事
1988年 オリエンタルモーター株式会社に入社、送風機の羽根・フレームの開発・設計に従事
2008年 法政大学にて学位取得、博士(工学)
2014年1月現在、オリエンタルモーター株式会社 技術支援部主席研究員
最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください


