装置設計者のための騒音の基礎 第26回
窓関数の補正
この連載では、製品開発・設計をされる方を対象に、騒音に関する基礎的な事項を説明しています。前回は、窓関数がリーケージエラーの抑制に有効であることと、窓関数処理によりスペクトルのピークが低下することを説明しました。今回は、スペクトルのピーク低下への対策、すなわち窓関数の補正について説明します。
窓関数に対する補正は、フーリエ解析の式に窓関数の式を組み合わせた式の係数を求めれば得られますが、複雑です。ここでは、エクセルを使って補正について考えてみます。具体的には、10Hzの正弦波に窓関数を行った波形と行う前の波形の、振幅およびパワーを計算して比較してみます。
図1に示すように、B列に10Hzで振幅1の正弦波を生成します。B2セルに、SUMSQ関数でB列の平方和を求めてデータ数で割ることで信号のパワーを求めます。B2セルの値は0.5となりますが、三角関数の公式からも振幅1のパワーは0.5となります。次に、C列にハニング窓を生成し、D列に窓関数処理済の信号を生成します。図2に窓関数処理前の信号波形を、図3に窓関数処理を行った信号波形を示します。
B列にフーリエ解析を行い、E列のフーリエ解析結果からF列に振幅を、G列にパワーを求めます。振幅はフーリエ解析結果の絶対値をデータ数で割った値を2倍します。また、パワーは、フーリエ解析結果の絶対値をデータ数で割った値を2乗して2倍します。同様に、D列にフーリエ解析を行い、I列に振幅を、J列にパワーを求めます。

図1 エクセルシートへの数式の入力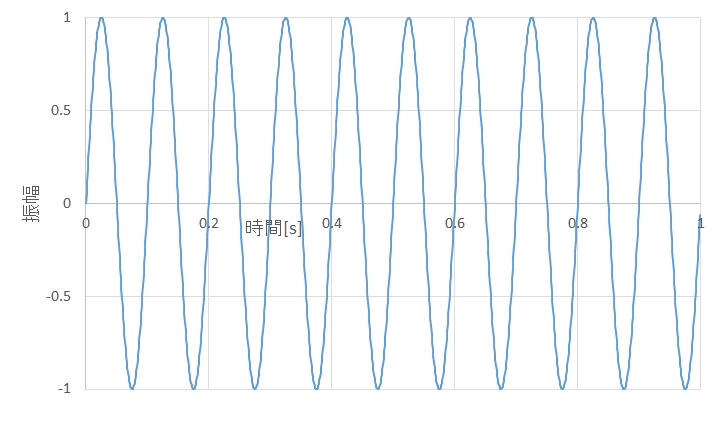
図2 信号波形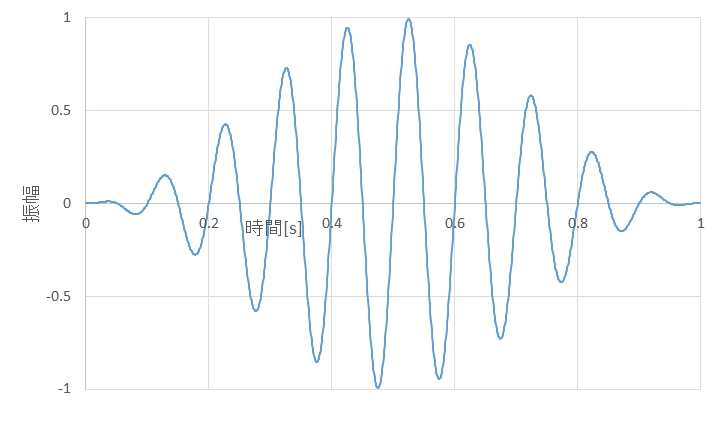
図3 窓関数操作を行った信号波形
図4に振幅のスペクトルを、図5にパワースペクトルを示します。図において、青色の線が元の信号のスペクトルで、橙色の線が窓関数処理を行った信号のスペクトルです。スペクトルのピーク前後すなわち、9、10、11Hzのスペクトルの値を表1に示します。図4および表1の振幅欄を見ると、元の信号では10Hzで1の振幅が、窓関数処理により、9Hzと11Hzに広がっていることがわかります。これは、周波数分解能が低下したことを意味します。また、窓関数処理後の振幅の9、10、11Hzの和は1となり、振幅そのものは変化していないことがわかります。一方、図5および表1のパワー欄を見ると、元の信号では10Hzで0.5のパワーが、窓関数処理により、9Hzと11Hzに広がっていることがわかります。しかしながら、その和は、振幅の場合とは異なり、0.1875と元の信号のパワーの0.5よりも低下しています。つまり、窓関数処理により、信号のパワーは、0.1875/0.5=3/8に低下します。あるいは、デシベル表示では、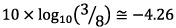 と、4.26dB低下します。この逆数が窓関数補正になり、ハニング窓処理を行った場合、パワースペクトルを8/3倍にすると、あるいは4.26dB加えると、元の信号のパワーと等しくなります。なお、8/3倍という補正は、ハニング窓の場合の補正であり、他の窓関数では、異なった補正値となります。
と、4.26dB低下します。この逆数が窓関数補正になり、ハニング窓処理を行った場合、パワースペクトルを8/3倍にすると、あるいは4.26dB加えると、元の信号のパワーと等しくなります。なお、8/3倍という補正は、ハニング窓の場合の補正であり、他の窓関数では、異なった補正値となります。
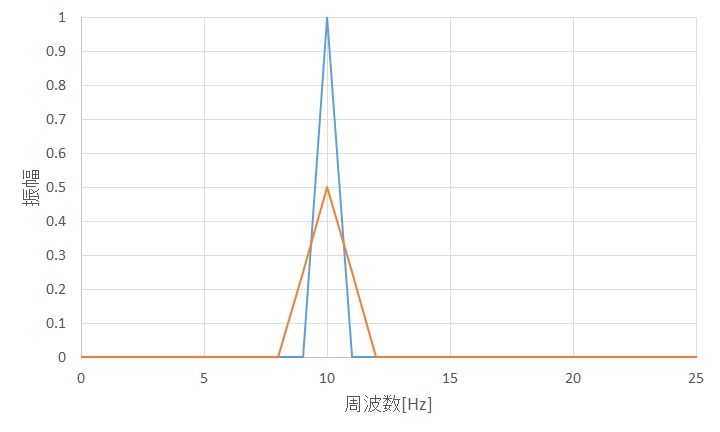
図4 振幅スペクトル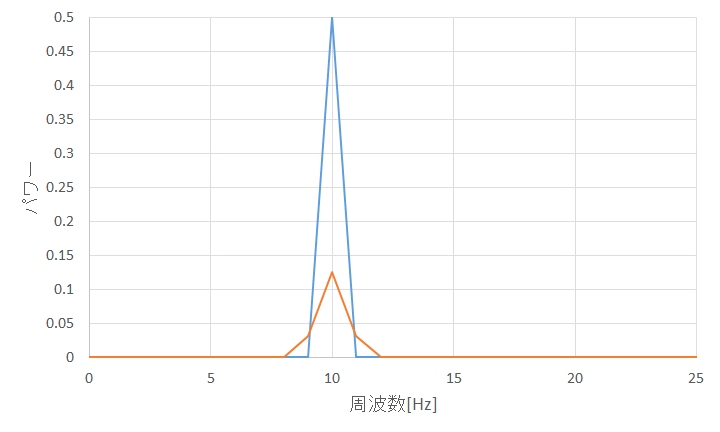
図5 パワースペクトル(青:窓関数なし、橙:窓関数あり)
| 窓関数なし | 窓関数あり | |||
|---|---|---|---|---|
| 周波数[Hz] | 振幅 | パワー | 振幅 | パワー |
| 9 | 0 | 0 | 0.25 | 0.03125 |
| 10 | 1 | 0.5 | 0.5 | 0.125 |
| 11 | 0 | 0 | 0.25 | 0.03125 |
窓関数には、ハニング窓以外にもいくつか種類があります。次回は、その他の窓関数について説明します。
【参考文献】 機械音響工学 鈴木ほか コロナ社

著者プロフィール
御法川 学 氏 | 法政大学 理工学部 機械工学科 教授
環境計量士(騒音・振動)
1992年 法政大学大学院 工学研究科 機械工学専攻
1992年 株式会社荏原総合研究所 入社
1999年 法政大学工学部 助手
2001年 東京工業大学にて学位取得、博士(工学)
2004年 法政大学工学部 助教授
2010年 法政大学理工学部 教授

著者プロフィール
伊藤 孝宏 氏 | オリエンタルモーター株式会社 技術支援部主席研究員
1982年 筑波大学基礎工学類卒業。新日本製鉄株式会社に入社、加熱・冷却設備の開発に従事
1988年 オリエンタルモーター株式会社に入社、送風機の羽根・フレームの開発・設計に従事
2008年 法政大学にて学位取得、博士(工学)
2014年1月現在、オリエンタルモーター株式会社 技術支援部主席研究員
最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください


