5.7 マトリックス解法

　各 要素 の値は隣り合う要素の値を使って表現されます。例えば、図5.20で要素3について考えた場合には以下のような式になります。

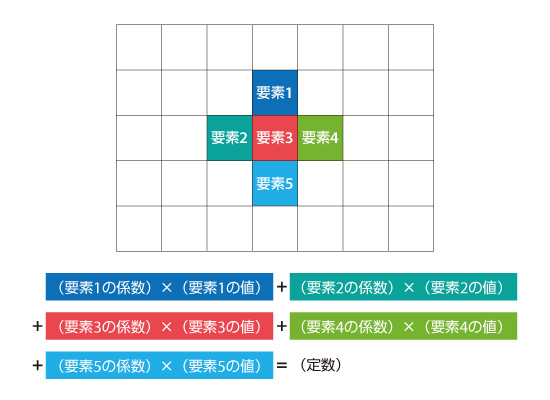
図5.20　隣接要素の位置関係と方程式

　上の図は2次元の例なので隣接する要素は上下左右の4つとなりますが、3次元の場合にはさらに前後方向にも隣接する要素があるため隣接する要素は合計で6つとなります。定数の部分には、 流れ の方程式であれば外力、 熱 の方程式であれば発熱量などの値が入ります。

　この関係式は要素の数だけ作られます。したがって、要素数が100万であれば、100万元の連立1次方程式を変数の数だけ解かなければいけません。この方程式群は行列形式で表現することができるため、行列の英訳である ”matrix” を使って、方程式の解法をマトリックス解法と呼ぶことがあります。その解法は大きく 直接法 と 反復法 と呼ばれる方法に分けられますが、 熱流体解析 では一般的に反復法が用いられます。
　ここでは、説明を簡単にするために2元連立1次方程式について、ヤコビ法という反復法を使った計算手順をご紹介します。以下の方程式について考えてみます。

この連立方程式の解は x = 3, y = 4 となります。
以降の計算をわかりやすくするため、式(1)を以下のように変形します。

これを反復法によって解く場合には、まずに初期値として適当なxとyの値を設定します。ここではxとyの初期値を0として式(2)に代入してみます。

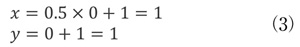
これによって、1回目の解はx = 1, y = 1 と求められます。次にこのxとyの値を再び式(2)に代入します。

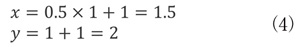
そうすると、2回目の解としてx = 1.5, y = 2 が得られ、先ほどのx =1, y = 1 より 厳密解 に近づいたことがわかります。この操作を繰り返していくと結果は以下の表のようになります。

表5.1　ヤコビ法の計算結果

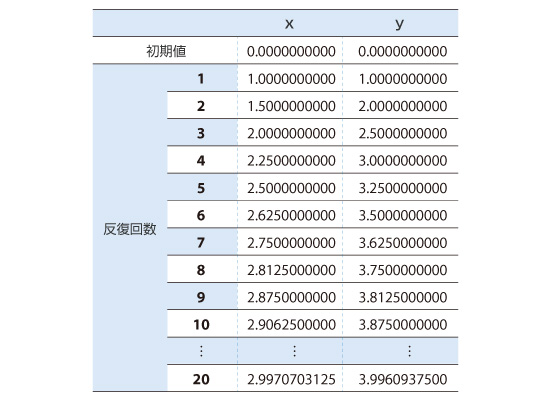
このように繰り返し計算を行っていくことで、xとyの値が連立方程式の解に近づいていくことがわかります。

　ここでは説明を簡単にするためにヤコビ法を使いましたが、一般にはより高速な反復法が使用されます。基本的には 反復回数 が多くなるほど厳密解に近い結果が得られますが、厳密解と完全に一致する結果を得ることは難しいことや、多くの問題では厳密解自体がわからないため、実際にはk－1回目と k 回目の計算結果の差が基準値より小さくなったところで計算を打ち切って解とします。この基準値のことを 収束判定 値といいます。収束が十分でない場合には妥当な結果が得られないこともあるため注意が必要です。

次回は、「第5章 熱流体解析の基礎(6)」についてご説明したいと思います。

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください