流体解析の基礎講座 第18回 第5章 熱流体解析の基礎:5.9.1 レイノルズ平均モデル(RANS), 5.9.2 ラージエディシミュレーション(LES)
5.9 乱流解析
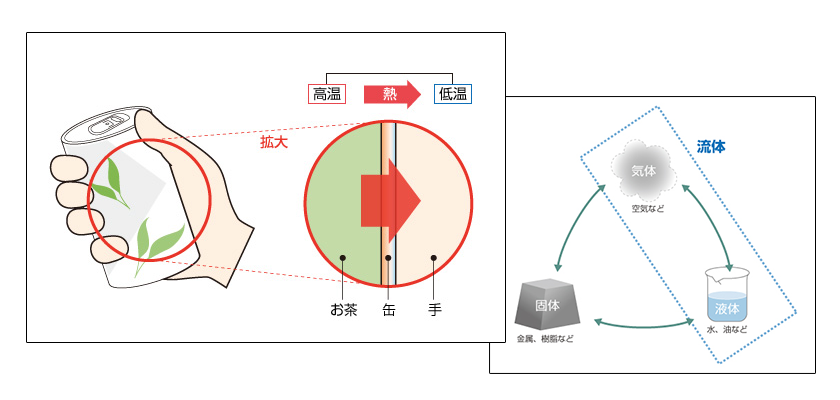
3.2.4 層流と乱流 で述べたように現実に見られる 流れ の多くは 乱流 となります。図5.23はその乱流のイメージを示したものです。一度発生した 渦 は分裂を繰り返し、より小さなスケールの渦へと変化していきます。そして、最終的に 粘性 によって熱エネルギーとなって消滅します。この過程によって流れ場には大小さまざまなスケールの渦が存在し、これらの渦によって流れや 温度 の分布が影響を受けます。
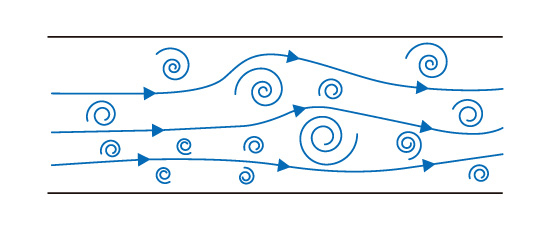
図5.23 乱流のイメージ図
乱流解析の手法はスケールの異なるこれらの渦の取り扱い方によって、大きく次の3種類に分類することができます。
以降では、これらの手法について簡単に説明していきます。
5.9.1 レイノルズ平均モデル(Reynolds Averaged Navier-Stokes: RANS)
流れを問題とする場合、工学的に重要なものは平均的な流れや温度の分布、あるいは物体に掛かる力の平均値などであることが大半です。そこで図5.24のように本来は非定常な現象である乱流現象の時間平均を調べる方法が考えられます。この平均化操作を レイノルズ平均 と呼びます。
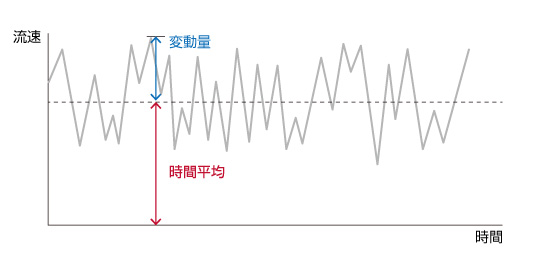
図5.24 レイノルズ平均
レイノルズ平均を施した方程式に基づいて平均的な流れのみを求める方法を ナビエ・ストークス方程式 のレイノルズ平均( Reynolds Averaged Navier-Stokes )の頭文字をとって、 RANS (ランズ)といいます。
レイノルズ平均を取った 支配方程式 には乱れの影響を示す レイノルズ応力 と呼ばれる項が含まれます。この項は平均流に対する乱れの効果を表していますが、平均化された方程式のみでは レイノルズ応力を求めることができないため、レイノルズ応力を表現するために何らかの近似を行う必要があります。この近似に用いられるものが一般的に 乱流モデル と呼ばれるもので、代表的なものとして標準k-εモデルなどがあります。
この方法では、 カルマン渦 のように非定常的な渦放出を伴う流れなど、平均流では評価できない流れ場の時間的な変化や乱流渦の構造などを表現することはできませんが、前述の3つの方法の中では最も計算負荷が低いことから、実用計算では数多く使用されています。
5.9.2 ラージエディシミュレーション(Large Eddy Simulation: LES)
小さな渦よりも大きな渦の方がより多くのエネルギーを持っているため、相対的に大きな渦のほうが流れ場に与える影響が大きいと考えられます。そこで基礎方程式に空間的なフィルターをかけ、フィルターのスケール以上の渦についてはモデル化を行わずに直接解き、それ以下の小さな渦の影響についてはモデル化して表現することが考えられます。簡単に言えば メッシュ のサイズに応じて渦をふるいにかけ、ふるいにかかったものを直接解くようなイメージです。このような方法を ラージエディシミュレーション(Large Eddy Simulation) の頭文字を取って LES (エルイーエス)といいます。
一般的にフィルターのサイズはメッシュ幅程度とされるため、直接計算される大きなスケールのことは グリッドスケール (grid scale, GS)、モデル化される小さなスケールのことは サブグリッドスケール (subgrid scale, SGS)と呼ばれます。
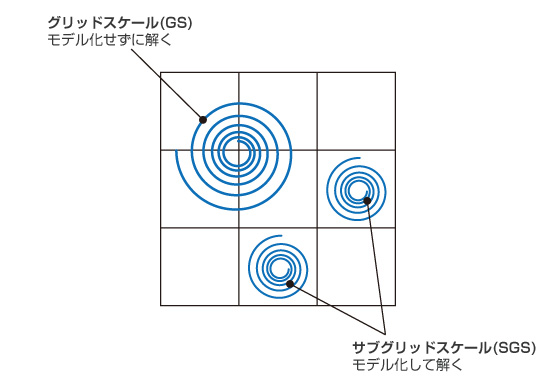
図5.25 グリッドスケールとサブグリッドスケール
メッシュ幅が小さいほどモデル化される度合いが小さくなるため、計算負荷は大きくなりますが、より現実に近い結果を得られる可能性が高いといえます。
次回は、「第5章 熱流体解析の基礎(8)」についてご説明したいと思います。

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士(工学)
学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。
最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください


