5.2 有限体積法

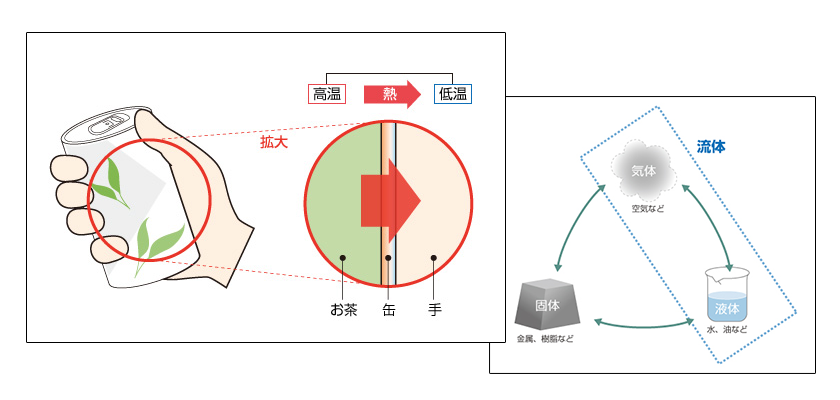
　 有限体積法（Finite Volume Method: FVM） は、分割されたそれぞれの空間において、流入量と流出量の差から空間に蓄えられる物理量を考え、解を求める方法です。

　イメージをつかむために、図5.4のような容器に水を注いでいる状態を考えてみます。ある時間の間に溜まる水の量（変化量）は流入量と流出量の差から求められます。溜まった水の量がわかれば、そこから水位がどのくらい変化するかを知ることができます。この水位の変化が求める量に相当します。

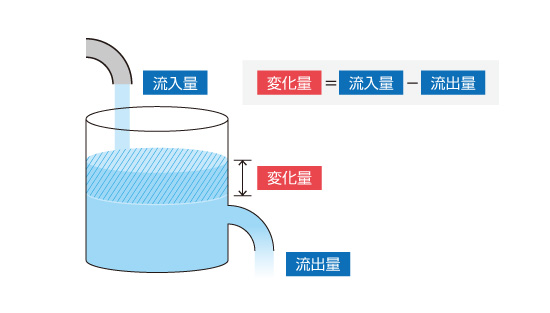
図5.4 有限体積法の考え方

　実際の解析では対象を複数の空間で分割するため、図5.5のように容器がいくつもつながっているような状態になります。

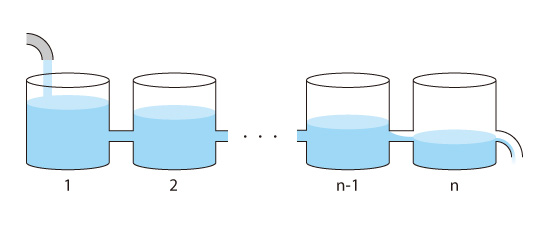
図5.5 複数の空間で分割した場合の例

そのため、容器から流出する量は隣の容器に流入する量と等しくなります。

　イメージをつかんだところで、もう少し具体的に見ていきたいと思います。 エネルギー保存式 から 温度 を求める場合には、 熱伝導 や 対流熱伝達 などによって空間に流入した 熱量 と空間から流出した熱量を考え、蓄えられた熱量から温度変化を求めます。

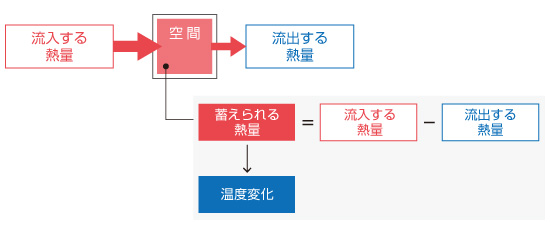
図5.6 空間への熱の出入り

　このような熱量の出入りが分割された各空間について計算され、最終的にそれぞれの空間における温度が求められます。

　図5.7には左端が高温、右端が低温となる場合の例を示しています。低温状態からスタートすると、始めた直後は各空間に流入する熱量のほうが多いため、左側から徐々に温度が上がっていきます。そして、十分時間が経過すると一番下の図のように各空間に出入りする熱量がつりあい、温度が変化しない状態（ 定常状態 ）となります。

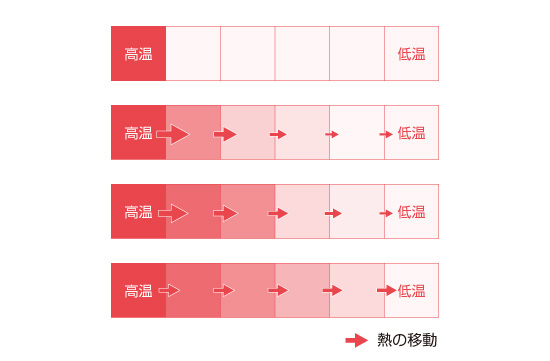
図5.7 熱の伝わり方と温度分布

　 流れ についても基本的な考え方は同じですが、流入する運動量と流出した運動量のほかに、 粘性 による作用、 圧力 による作用を考えて流速変化を求めます。

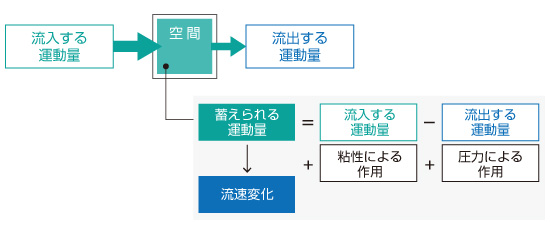
図5.8　空間への運動量の出入り

ただし、圧力だけは 基礎方程式 が存在しないため求め方が異なります。
圧力の求め方にはいくつかの方法がありますが、仮の圧力を使用して 流速 を計算し、その流れが 連続の式 を満たすように圧力を補正するといった方法などが採られます。

　次回は、「第5章 熱流体解析の基礎(3)」についてご説明したいと思います。

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください