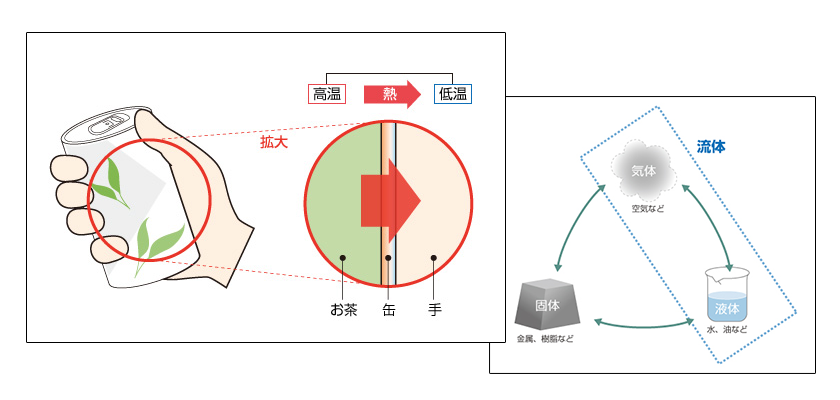
第5章では、熱流体解析 の基本的な考え方や解析の流れについてご紹介します。

5.1 基礎方程式と離散化

　 流体 や 熱 の移動現象は微分方程式によって記述されます。以降では 非圧縮性流体 について考えることにすると、方程式として以下のものが挙げられます。

• ナビエ・ストークス方程式 （運動量保存式 ）
• 連続の式
• エネルギー保存式

　ナビエ・ストークス方程式と連続の式は流体の運動、エネルギー保存式は熱の移動現象を記述した方程式です。これらの方程式は熱流体解析における基礎となるもので、 基礎方程式 （または 支配方程式 ）と呼ばれます。
　基礎方程式を理論的に解くことができれば、即座に 流れ や 温度 の分布が得られますが、現在のところ、限られた場合を除いてこれらの方程式の理論解は得られていません。 そこで登場するのが、基礎方程式をコンピュータによって数値的に解く熱流体解析ということになります。しかし、このときに問題となるのが、コンピュータは連続した値を扱うことができないということです。

そのため、基礎方程式を離散的な値を使った表現に書き換える必要があります。このことを 離散化 といいます。

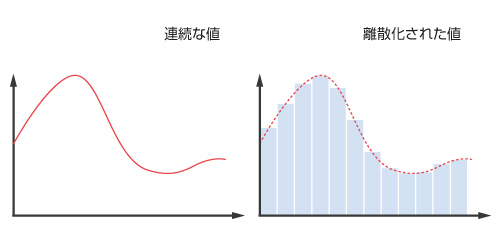
図5.1　離散化の例

　イメージを掴むために天気を例にとって考えてみます。天気も連続的に変化するため、このままではコンピュータで扱うことができません。

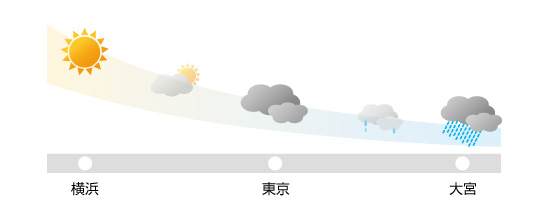
図5.2　実際の天気

　そこで、コンピュータで扱えるように天気を考える地点を決め、ある場所の天気とその周囲の天気の関係を求めます。この関係を導き出す作業が離散化に当たります。例えば離散化の結果、ある地点の天気は周囲の天気の平均で与えられる、という関係が得られたとすると、横浜の天気が晴れで、大宮の天気が雨の場合には、コンピュータでその平均をとることによって東京の天気がくもりと求められるわけです。

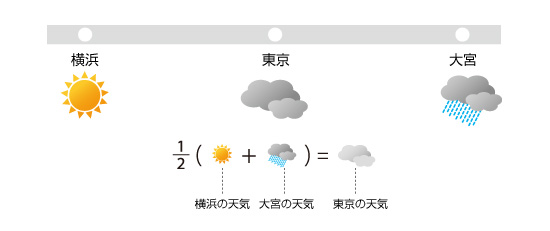
図5.3　コンピュータで扱う天気

　上の例では平均で考えましたが、熱流体解析ではもう少し複雑な方法で周囲の情報との関係を導き出します。このときに用いられる離散化方法にはいくつかありますが、代表的なものとして、次のような方法があります。

• 有限差分法 （Finite Difference Method: FDM） ※ 単に 差分法 と呼ばれる場合もあります
• 有限体積法 （Finite Volume Method: FVM）
• 有限要素法 （Finite Element Method: FEM）

　多くの商用の熱流体解析ソフトウェアでは、有限体積法に基づいた離散化が用いられています（有限体積法については次節で説明します）。基礎方程式は微分方程式ですが、離散化を行うことによって、隣り合う空間どうしの関係を代数方程式（四則演算で記述される方程式）で表現できるようになります。
　ビルや車などの周りに生じる風の流れや室内の温度分布といった現象を熱流体解析によって再現するためには、まず空間を 要素 とよばれる小さな領域に分割し、上記のような方法で離散化された基礎方程式を適切な 境界条件 や 初期条件 のもとで解く必要があります。その結果として、ナビエ・ストークス方程式と連続の式からは 流速 と 圧力 、エネルギー保存式からは温度が得られます。

　次回は、「第5章 熱流体解析の基礎(2)」についてご説明したいと思います。

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください