3.2.4 層流と乱流

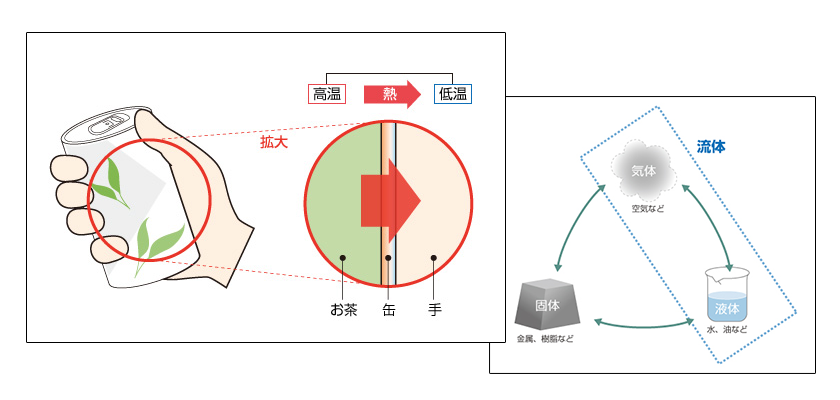
　 流れ には層流と乱流という2つの状態があります。 層流 は 流体 が規則正しく運動している流れのことです。それに対して流体が不規則に運動している乱れた流れは 乱流 と呼ばれます。
　身近な例としては図3.15のように、水道の蛇口から流れ出る水が挙げられます。水道のバルブを少しだけ開いたときには (a) のように水はまっすぐに流れ落ちますが、バルブの開度を大きくするにつれて、次第に液面が波打ち、(b) のような乱れた流れへと変化していきます。前者の流れが層流、後者の流れが乱流に相当します。

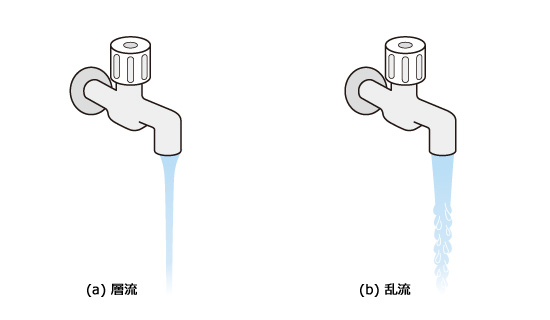
図3.15　蛇口から流れ出る水

　層流と乱流の明確な区別は1883年、イギリスの科学者オズボーン・レイノルズ（Osborne Reynolds, 1842-1912）の実験によってなされました。今日では レイノルズの実験 として知られるこの実験では、図3.16のように水が流れる円管内にインクを注入して流れの可視化が行われました。その結果、 流速 が小さいときにはインクは (a) のようにほぼ一本の直線状となって下流へ流れ、層流となりますが、流速が大きくなるとインクは (b) のように途中で乱れて円管全体に拡散され、乱流となることがわかりました。

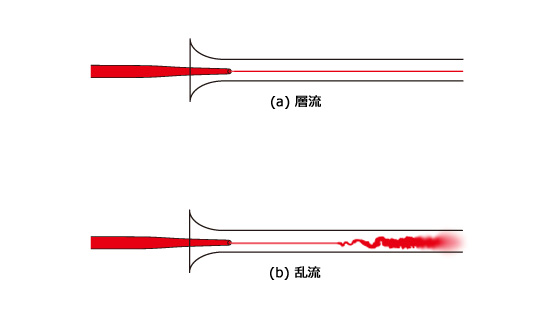
図3.16　レイノルズの実験

　レイノルズはこの実験から、流れが層流になるか、乱流になるかは レイノルズ数 という 無次元数 によって整理されることを見出だしました。 代表長さ （円管では内径）を L、 代表流速 （円管では断面平均流速）を U、 流体 の 密度 および 粘性係数 をそれぞれ ρ と μ とすると、レイノルズ数 Re は以下の式によって定義されます。

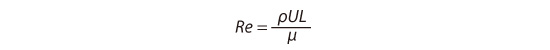
　レイノルズ数は分母が粘性力、分子が慣性力を表しており、流れにおける両者の相対的な影響力を示しています。幾何学的に相似な2つの流れで両者のレイノルズ数が同じであれば、粘性力と慣性力の割合が等しいことから、2つの流れは本質的に等しくなります。このことは レイノルズの相似則 と呼ばれます。
　例えば、図3.17のように50 km/h で走行する自動車の周りの空気の流れを 1/2の大きさの模型を使った風洞実験で再現したい場合には風速を2倍、すなわち 100 km/h とすればよいことがわかります（ただし、厳密には地面を同じ速度で動かす必要があるため、実車と風洞実験を完全に一致させることは容易ではありません）。

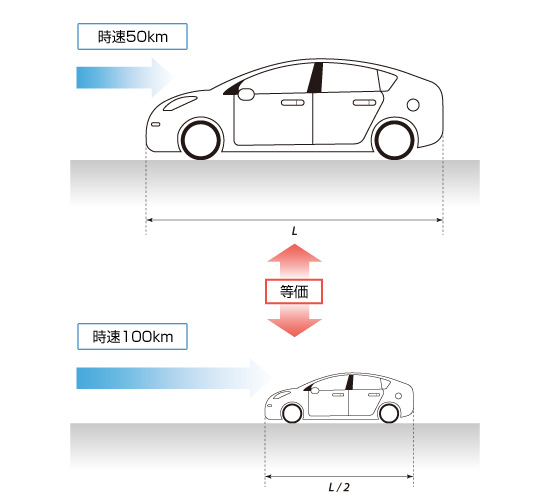
図3.17　レイノルズの相似則

　レイノルズ数の定義式からもわかるように、流体の粘性係数が大きい場合や流速が小さい場合には粘性力が支配的となるため、レイノルズ数は低く、流れは層流となります。一方、流体の粘性係数が小さい場合や流速が大きい場合には慣性力が支配的となるため、レイノルズ数は高く、流れは乱流となります。
　なお、流れの状態が層流から乱流に 遷移 するレイノルズ数は円管内の流れの場合、2,000 ～ 4,000 程度というのが一つの目安になります。しかし、この値は流れの状態や条件などによって大きく異なるため、あくまでも目安ということに注意してください。
　それでは、最後に身の回りで見られる流れが層流か乱流かを考えてみたいと思います。図3.18に示すように自転車が走っている状態を考えてみます。

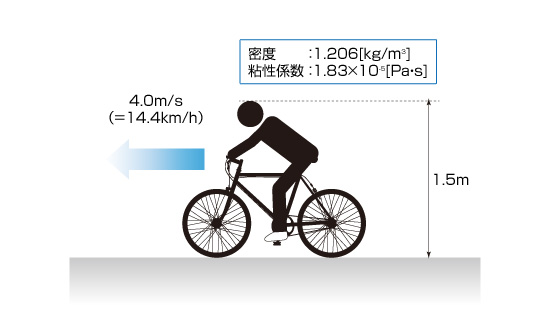
図3.18　自転車に乗る人の例

周りにある流体は空気であるとして、レイノルズ数を計算してみます。

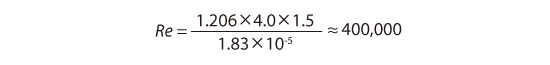
　この結果、レイノルズ数は約40万となり、先ほど目安として紹介した2,000を大きく上回っていることがわかります。この結果からも想像できるように、身近に見られる流れの多くは乱流となります。
　乱流には抵抗や騒音を増大させてしまうデメリットもありますが、一方で熱伝達や混合を促進するというメリットも兼ね備えています。そのため、製品の設計にあたっては乱流を適切に制御することが重要となります。

　次回は、「第4章 熱の基礎(1)」についてご説明したいと思います。

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください