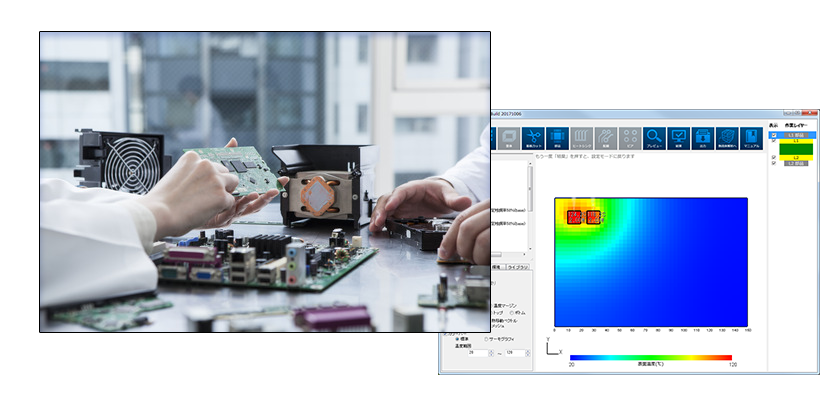
LTspiceのような 回路シミュレーター を使えば、回路設計に関する知識を持っていなかったとしても、電子部品の発熱量をある程度求めることが可能です。しかし、電子部品や電子回路に関連した知識を持つことで、シミュレーターをより使いこなせるようになります。そこで、今回から数回にわたって、電子工学の基礎を紹介していきます。

オームの法則

　 オームの法則 は「電子回路に 電流 が流れたときに、回路の2点間に発生する 電圧 はその2点間を流れる電流に比例する」というものです。この比例定数のことを 電気抵抗 または単に 抵抗 といい、その単位は Ω です。電圧を V [V], 電流を I [A], 抵抗を R [Ω] とすると、オームの法則は式(4.1)で表すことができます。

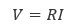(4.1)

　例えば、10 Ω の電気抵抗に 1 A の電流が流れると、電気抵抗の両端には 10 V の電圧が生じます。ただし、このように簡単に考えられるのは 直流 の場合に限られます。

直流と交流

　直流とは、時間が経過しても流れる向きが変化しない電流のことです。これに対して、時間の経過に伴って流れる向きが周期的に変化する電流のことを 交流 といいます。日本の商用電源は交流で供給されているため、電化製品のプラグをコンセントに挿すときに向きを意識する必要がありません。

　交流において、電流の波形が1秒間あたりに繰り返される回数を 周波数 といいます。コンセントから供給される電源の周波数は東日本で50 Hz、西日本で60 Hzですが、これは1秒間に波形がそれぞれ50回と60回繰り返されていることを表しています。繰り返しの様子を示すと図4.1のようになります。

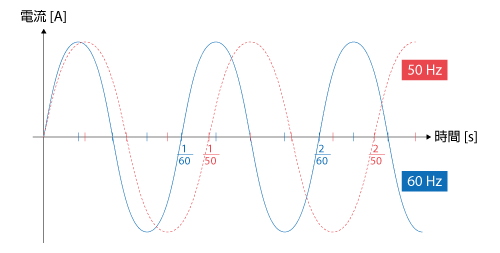
図4.1　50 Hzと60 Hzの交流の波形

交流の場合のオームの法則

　では、交流の場合のオームの法則を考えてみます。いま、t 秒における電流が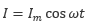で表されるとします。この Im< のことを 振幅 といいます。また、ω のことを 角周波数 といい、単位は rad/s です。角周波数は周波数 f [Hz] に 2π を掛けることによって得られ、その関係を示すと式(4.2)のようになります。

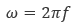(4.2)

電気抵抗については、直流であっても交流であってもそれ自体の大きさは変わりません。したがって、オームの法則の電流を先ほどのもので置き換えると、式(4.3)のようになります。

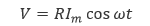(4.3)

しかし、式(4.3)のように 三角関数 を用いた表現では、回路が複雑になるにつれて計算が煩雑になります。そのため、複素数 を使って取り扱いを簡単にする方法がよく用いられます。このような方法を 複素記号法 といいます。今度は電流を式(4.4)のように表します。

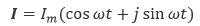(4.4)

j は 虚数単位 と呼ばれ、j² = -1となります。虚数単位は一般に i で表現されますが、電気・電子工学では電流に i を用いるため、混同を避けるために虚数単位に j を用います。式(4.4)は オイラーの公式 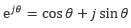を用いると式(4.5)のように書き換えられます。

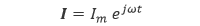(4.5)

左辺の I がボールド（太字）になっていますが、これは複素数であることを表しています。以降ではこのように複素数をボールドで表すことにします。指数関数 を用いることによって微積分を容易にするというのが複素記号法の狙いです。観測される値は計算結果の 実部 に対応します。例えば、電圧は複素数で表された電流と複素数で表された抵抗との積の実数成分に相当するというわけです。

　次回は、複素数表示を使ってもう少し複雑な交流回路を考えていきます。

著者プロフィール
CrEAM（Cradle Engineers for Accelerating Manufacturing)

電子機器の熱問題をなくすために結成された3ピースユニット。 熱流体解析コンサルタントエンジニアとしての業務経験を生かし、 「熱設計・熱解析をもっと身近なものに。」を目標に活動中。

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください