今回は前回よりも少し複雑な交流回路について考えていきます。

RLC直列回路

　図5.1に示す 電気抵抗 R と インダクタンス L のコイルと キャパシタンス（静電容量）C の コンデンサをつないだ直列回路を考えます。このような回路を3つの頭文字を取って、RLC直列回路 といいます。なお、電気抵抗の単位は Ω、インダクタンスの単位は H（ヘンリー）、キャパシタンスの単位は F（ファラッド）です。

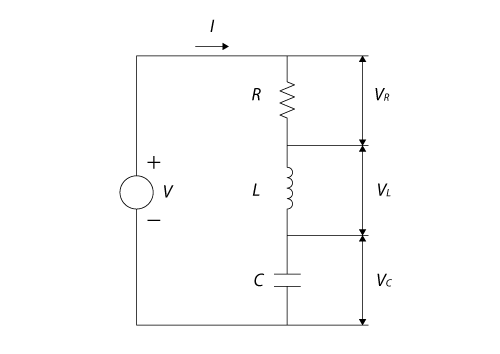
図5.1　RLC直列回路

インピーダンス

　図5.1の回路に交流電圧 V を印加し、電流 I = Ime^jωt が流れている場合を考えてみます。電気抵抗の両端に発生する 電圧 VR は オームの法則 から式(5.1)で与えられます。

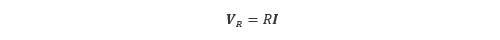(5.1)

コイルの両端に発生する電圧 VL は、インダクタンスとコイルを流れる電流の時間変化に比例し、式(5.2)で与えられます。

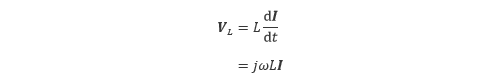(5.2)

　コンデンサの両端に発生する電圧 VC は、ある時間までに蓄積された電荷に比例し、キャパシタンスに反比例するため、式(5.3)で与えられます。

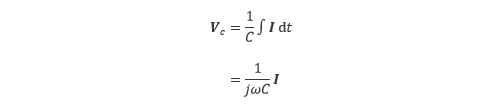(5.3)

直列回路では、全体の電圧は各電圧の和で与えられます。したがって、電圧と電流の関係は式(5.4)のようになります。

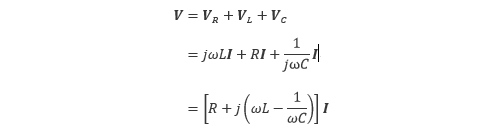(5.4)

式(4.4)の [] の中を Z と表すことにすると、Z は式(5.5)のように書き換えられます。

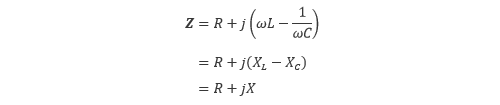(5.5)

この Z を インピーダンス といいます。また、第1項の R は電気抵抗のインピーダンス成分で レジスタンス と呼ばれます。また、第2項 XL= ωL はコイルのインピーダンス成分で 誘導リアクタンス、第3項 XC= 1/ωC はコンデンサのインピーダンス成分で 容量リアクタンス と呼ばれ、これらをまとめた X は単に リアクタンス と呼ばれます。このインピーダンスを用いることで、電圧と電流の関係は式(5.6)のようにまとめられます。

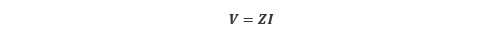(5.6)

式の対応関係を見るとインピーダンス Z は、オームの法則の電気抵抗に相当することがわかります。ここから、電流は式(5.7)で与えられます。

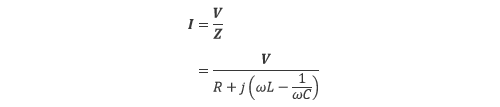(5.7)

この式より、電流は 周波数 によって変化することがわかります。特に ωL=1/ωC、すなわち 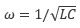 の関係が成り立つときにインピーダンスは純粋な電気抵抗と等しくなり、最小値をとります。このときに電流が最大となりますが、この周波数  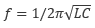のことを 共振周波数 といいます。

　次回は、インピーダンスが電圧と電流の位相差に及ぼす影響を考えていきます。

著者プロフィール
CrEAM（Cradle Engineers for Accelerating Manufacturing)

電子機器の熱問題をなくすために結成された3ピースユニット。 熱流体解析コンサルタントエンジニアとしての業務経験を生かし、 「熱設計・熱解析をもっと身近なものに。」を目標に活動中。

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください