今回は、インピーダンスが電圧と電流の位相差に及ぼす影響を考えていきます。

電圧と電流の位相のずれ

　前回に引き続き、電気抵抗 R と インダクタンス L のコイルと キャパシタンス（静電容量）C の コンデンサをつないだ RLC直列回路 を考えていきます。前回示したように、この回路における 電圧 と 電流 の関係は式(6.1)で与えられます。

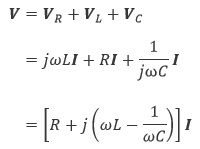(6.1)

　式(6.1)に電流 I = Ime^jωt を代入して整理すると、式(6.2)が得られます。

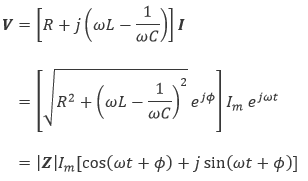(6.2)

ここで Φ は 位相角 と呼ばれ、式(6.3)で表されます。

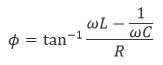(6.3)

また、式(6.2)の実部を取ることによって、電圧 V は式(6.4)で与えられます。

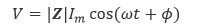(6.4)

式(6.4)から電流波形と電圧波形の 周波数 は同じであるものの、波形には位相角の分だけずれが生じることがわかります。具体的には、位相角 Φ が正の場合には電流よりも電圧の位相が進み、逆に負の場合には電流よりも電圧の位相が遅れます。

　では、式(6.2)を図示した図6.1を使ってもう少し詳しく見ていきます。図の左側には複素平面（縦軸が実軸、横軸が虚軸）、右側には交流の波形を示しています。時刻 t = 0 では、電流は実数成分のみの Im となるため、図中の○に対応します。そして、電流および電圧は時間の経過とともに、原点を中心として複素平面内を反時計方向に回転していきます。

(i) の  すなわち ωL=1/ωC の場合には、電圧と電流は同じ位相（同相）で変化していきます。(ii) の すなわち ωL > 1/ωC の場合には、電圧は電流の未来の状態と同じであり、位相が進むことがわかります。(iii) の  すなわち ωL ＜ 1/ωC の場合には、電圧は電流の過去の状態と同じとなり、位相は遅れることになります。

また、周波数が変化する場合には共振周波数 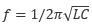 を境に位相が進みから遅れ、あるいは遅れから進みへと反転することがわかります。

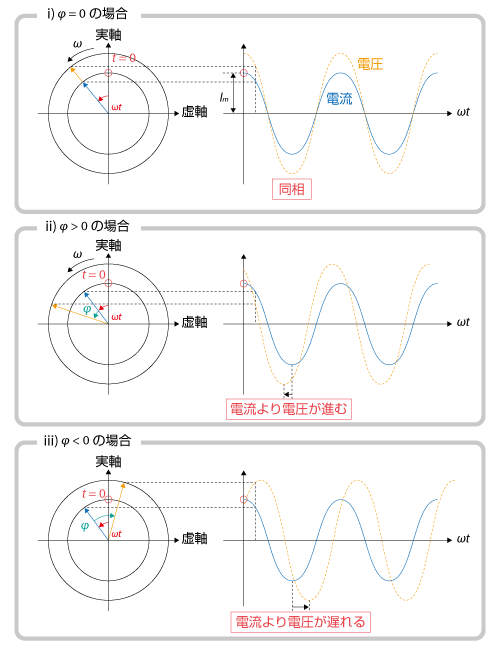
図6.1　電圧と電流の位相

手計算で位相のずれを予想

　RLC直列回路に周波数 50 Hz で 振幅 10 V の正弦波電圧が印加された場合の電流値を手計算で求めてみましょう。ここでは、電気抵抗を 1 Ω、インダクタンスを 1 mH、キャパシタンスを 1 mF とします。

　電圧の振幅は Vm=|Z| Im で求められます。第5回の式(5.5)を用いると |Z|≈3.04 となるので、Im≈3.3 [A] とわかります。また、式(6.3)より位相角は 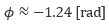 と求まります。1.24/2π≈0.2 ですので、電流は電圧に対して1/5波長ほど位相が進むと予想されます。

LTspiceを用いてシミュレーションしてみよう

　最後に LTspice で電流をシミュレートしてみましょう。図6.2に作成した回路図を示します。2波形分をシミュレートすると、図6.3に示す結果が得られます。緑色で示す電圧波形に対して、青色の電圧波形のピークは3.3 Aとなり、先ほどの手計算と一致していることがわかります。また、電流波形は電圧波形の左側になっており、電流は電圧に対して位相が進んでいることがわかります。

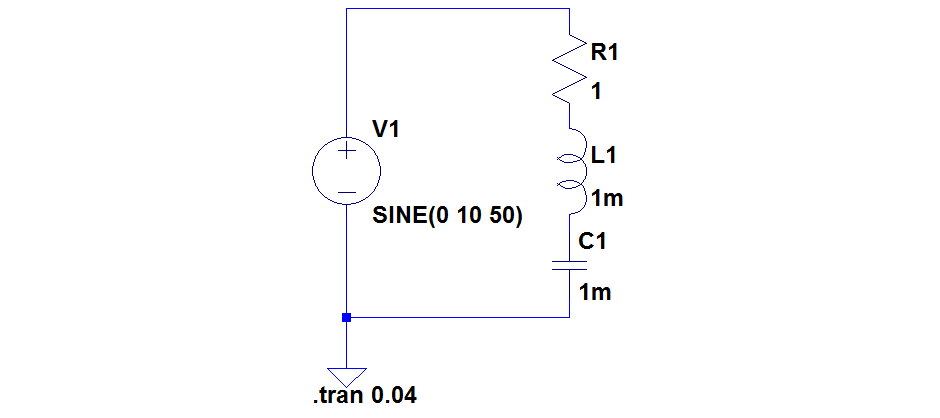
図6.2　LTspiceで作成したRLC直列回路

図6.3　電圧波形と電流波形

　　次回は、電流と発熱量の関係について見ていきます。

著者プロフィール
CrEAM（Cradle Engineers for Accelerating Manufacturing)

電子機器の熱問題をなくすために結成された3ピースユニット。 熱流体解析コンサルタントエンジニアとしての業務経験を生かし、 「熱設計・熱解析をもっと身近なものに。」を目標に活動中。

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください