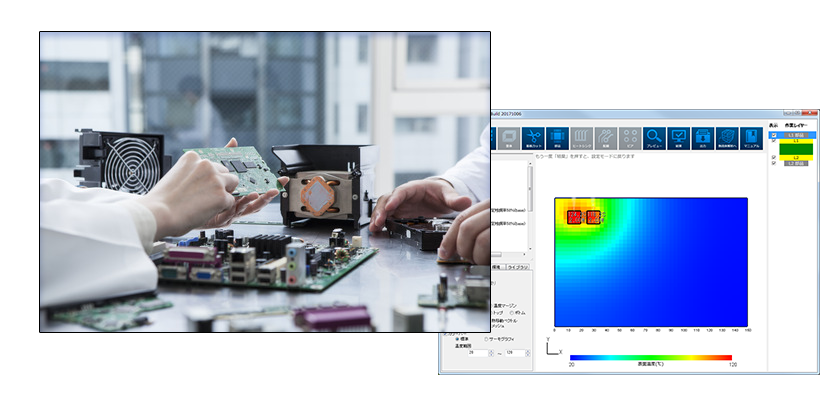
今回は、電流と発熱量の関係を見ていきましょう。

ジュールの第一法則

　導体中を 電流 が流れると、物質を構成する原子や分子と電子が衝突します。この衝突によって、電子のエネルギーは失われ、その分原子や分子の熱エネルギーが増加するため、電流が流れている導体では熱が発生します。この熱を ジュール熱 といいます。

　導体を流れる電流と発生する熱量の関係を表した法則を ジュールの第一法則 といいます。導体の 電気抵抗 を R [Ω]、電流を I [A]、電流が流れる時間を t [s] とすると、発熱量 Q [J] は以下の式で表されます。

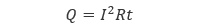(7.1)

電子部品の発熱量は単位時間あたりの発熱量 W で表され、その単位は W (= J/s) です。これは、式(7.1)の両辺を時間 t で割ったものになります。また、導体の両端に発生する 電圧 V が電流 I と電気抵抗 R の積で表されること（オームの法則）を用いると、式(7.1)は以下のように書き換えられます。

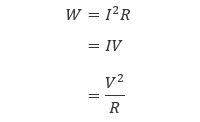(7.2)

　この式を用いることで発熱量が求められます。例えば、ダイオードに 0.5 A の直流電流が流れ、0.1 V の電圧降下が生じているならば、発熱量は 0.5 × 0.1 = 0.05 Wとなります。

交流の場合の発熱量

　交流の場合には 実効値（または rms値）を用いて計算します。実効値とは、電気抵抗に交流が流れたときに消費される1周期あたりの平均電力と、等しい電力を消費する直流の電流もしくは電圧のことです。

電気抵抗 R に電流 I が流れたときに消費される電力は I²R で与えられます。したがって、振幅 Imの正弦波交流（周期 T）の実効値を Ieとすると、両者の関係は式(7.3)のようになります。

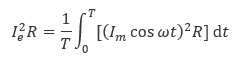(7.3)

上式の右辺は1周期分の消費電力を表しており、この式を整理していくことで式(7.4)が得られます。

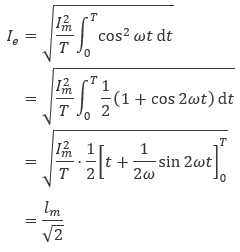(7.4)

この結果から、実効値は 振幅 の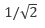倍になることがわかります。ここでは、電流について示しましたが、電圧についても同様の関係が成り立ちます。

　例として、ダイオードに振幅 0.5 A の交流電流が流れ、0.1 V の電圧降下が生じている場合を考えると、ダイオードの電圧降下は電流によらずほぼ一定となること、そして逆方向には電流は流れないことから、発熱量は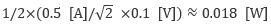となります（厳密にはごくわずかに逆方向の電流（漏れ電流 もしくは ドリフト電流 といいます）を生じますが、ここでは無視しています）。波形が正弦波ではない場合には数値的に積分する必要がありますが、LTspiceなどの回路シミュレーターを用いることによって、計算することができます。

　次回は、入出力インピーダンスについて説明します。

著者プロフィール
CrEAM（Cradle Engineers for Accelerating Manufacturing)

電子機器の熱問題をなくすために結成された3ピースユニット。 熱流体解析コンサルタントエンジニアとしての業務経験を生かし、 「熱設計・熱解析をもっと身近なものに。」を目標に活動中。

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください