もっと知りたい! 熱流体解析の基礎42 第5章 物質拡散:5.2.4 物質量基準の濃度
5.2.4 物質量基準の濃度
物質量 に基づく 濃度 の単位には モル濃度 と モル分率 があります。
モル濃度
モル濃度は、単位体積の混合物に含まれる成分の物質量のことで、単位は mol/m3 です。図5.7のように 1 L(= 0.001 m3 )の食塩水に 0.1 mol の食塩が含まれている場合を考えると、モル濃度は以下のようになります。

なお、Naの原子量は 23、Cl の原子量は 35.5 なので、食塩(NaCl)1 molあたりの質量は 23 + 35.5 = 58.5 [g] となります。したがって、上の例は1 L の食塩水に5.85 g の食塩が含まれている場合と等しくなります。
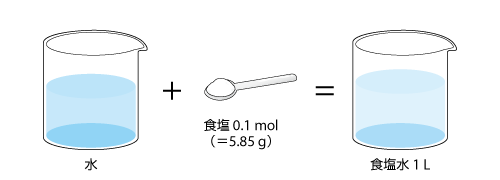
図5.7 食塩水とモル濃度
モル分率
モル分率は、単位物質量の混合物に含まれる成分の物質量のことで、単位を持たない無次元量です。しかし、モル分率であることを明確にするために、mol/mol という表記が用いられることもあります。図5.8のように 99.5 mol の水に 0.5 mol の食塩を溶かす場合を考えると、モル分率は以下のようになります。

なお、Hの原子量は 1、Oの原子量は16なので、水(H2 O)1 mol あたりの質量は 1 × 2 + 16 = 18 [g] となります。一方、食塩(NaCl)の質量は先に書いたように58.5 [g] となります。したがって、上の例は 18 g/mol × 99.5 mol = 1,791 g の水に、58.5 g/mol × 0.5 mol = 29.25 g の食塩を溶かす場合と等しくなります。
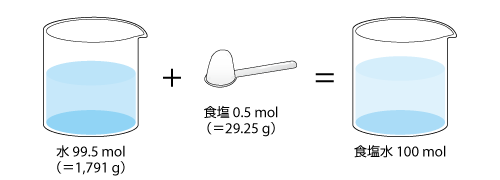
図5.8 食塩水とモル分率
もっと知りたい 濃度の変換
質量濃度とモル濃度の間には、以下の関係が成り立ちます。

これを用いて、先ほどのモル濃度を質量濃度に換算すると、以下のようになります。

さて、混合物全体の質量濃度やモル濃度は、各成分の和に等しくなります。混合物が n 種類の成分から構成されるとすると、その関係は以下の式で与えられます。
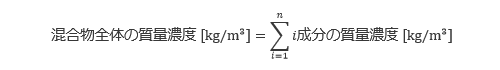
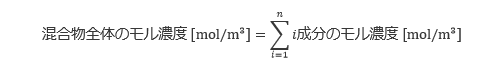
質量分率やモル分率は、混合物全体の質量濃度やモル濃度に対する、ある成分の質量濃度やモル濃度の割合を示し、その関係は以下の式のようになります。


また、混合物を構成する各成分の質量濃度やモル濃度の和は、混合物全体の質量濃度やモル濃度と等しくなるために、質量分率やモル分率のそれぞれについて各成分の和を取ると1となります。

先ほどの例では、2つの物質の混合物である食塩水を考えましたが、3種類以上の混合物についても考え方は同じです。
もっと知りたい 理想気体のモル分率
理想気体の状態方程式 は、> を T [K]、圧力 を p [Pa]、物質量を n [mol]、体積を V [m3 ] とすると以下の式で表されます。
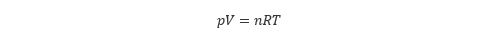
ここで、R は 一般気体定数 と呼ばれ、R = 8.314 J/(mol・K) です。理想気体の状態方程式に従う気体を 理想気体 や 完全気体 といいます(理想流体 と混同しないように注意してください)。実在する気体は厳密な理想気体ではありませんが、身の回りにおける空気などは理想気体と見なすことができます。
さて、n 種類の理想気体を混合したとします。この混合気体の圧力を 全圧 、混合気体のある成分が同じ体積を単独で占めたときの圧力を 分圧 といいます。混合気体の成分 i の分圧を pi [Pa]、物質量を ni [mol] とすると、各成分に対しても以下のように理想気体の状態方程式が成立します。
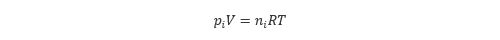
成分 i の物質量 ni [mol] を全体の体積 V [m3 ] で割ったものはモル濃度 Ci [mol/m3 ] であることから、状態方程式を以下のように変形したものはモル濃度となります。
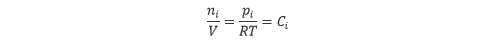
したがって、モル分率は以下のように書き換えることができます。
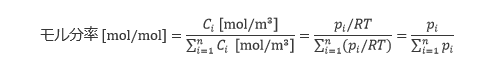
ところで理想気体の混合気体では、全圧は各成分の分圧の和で表されます。これを ドルトンの法則 といい、以下の式で表されます。
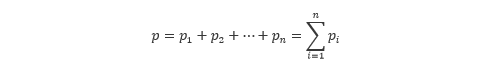
仮に標準大気圧(101,325 Pa)の空気中を占める窒素と酸素の体積割合がそれぞれ 79 % と 21 % であるすると、ドルトンの法則は図5.9に示すようになります。
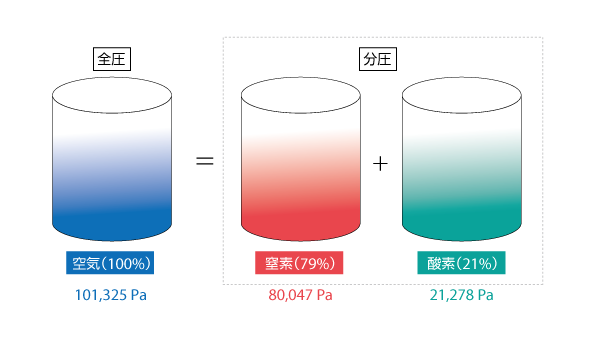
図5.9 ドルトンの法則
ドルトンの法則を用いることで、モル分率は以下のように書き換えられ、理想気体の混合気体では、モル分率は全圧に対する分圧の割合でも表されることが分かります。
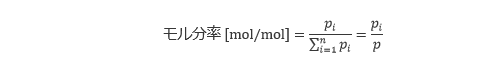

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士(工学)
学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。執筆したコラムに「流体解析の基礎講座」がある。
最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください


