今回からフーリエ解析を行う際の基本事項について説明します。今回は、フーリエ解析の概要について説明します。

　フーリエ解析は、信号を正弦波関数の組合せにより周波数成分に分解する手法を言います。例えば、音あるいは振動を低減することを考えてみます。計測の結果、図1に示すような波形が得られたとしても、このままでは、2msピッチの繰り返しが大きそうだというくらいの手がかりしか得られません。そこで、この信号波形にフーリエ解析を行うと、図2に示すような結果が得られ、周波数が1500Hzの成分が最大であることがわかります。したがって、1500Hzの発生源がないか、あるいは、1500Hzでの共振が起きていないかを検討するといった具体的な方針が立てられます。図2は周波数スペクトルとも呼ばれ、一連の解析はスペクトル解析とも呼ばれます。

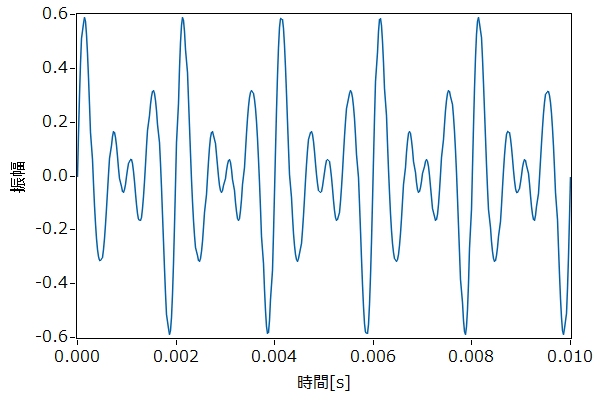
図1　信号波形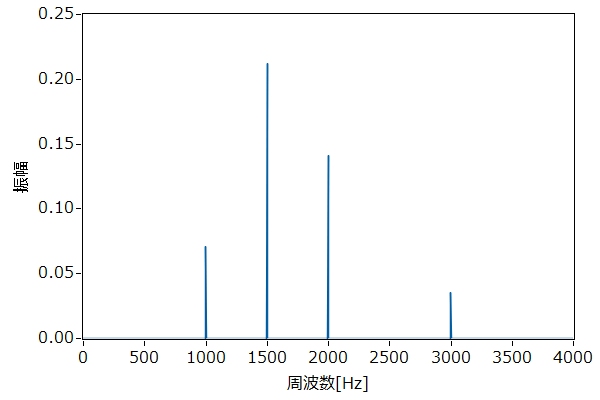


図2　フーリエ解析結果

　ここで、用語について簡単に説明します。数学の分野では、フーリエ解析は、関数をフーリエ級数に展開することを言います。これに対して、工学分野では、フーリエ解析は、離散化された信号を周波数成分に変換する手法、すなわちDFT(Discrete Fourier Transform、離散フーリエ変換)を指します。DFTのうち、データ数が2のべき乗のときにフーリエ変換を高速化できる手法がFFT(Fast Fourier Transform、高速フーリエ変換)です。

　FFTアナライザあるいはFFT解析ソフトは、信号波形から周波数スペクトルへの変換を自動で行うため、利用者は、フーリエ変換について理解する必要はありません。しかしながら、結果を解釈したり、より良い解析を行ったりするためには、フーリエ解析についてのある程度の知識は必要となります。

　次回から、DFTの実際、ナイキストの標本化定理と周波数スペクトルとの関係、時間波形と周波数スペクトルとの量的関係を示すパーシバルの定理とパワースペクトル、窓関数といったことについて説明します。

　次回は、エクセルを用いてFFT処理を行ってみます。

【参考文献】 機械音響工学　鈴木ほか　コロナ社