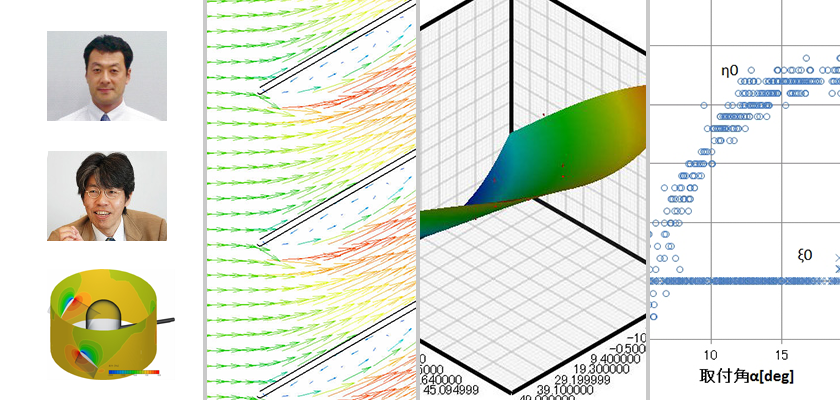
今回から、模型飛行機の設計として主翼とプロペラの最適な翼断面形状をEOoptiとSCRYU/Tetraを用いて検討した例を紹介します。主翼の検討では、揚力係数・抗力係数についての説明、ジューコフスキー翼の作図法についての説明、モデルの作成、最適解探索結果についての3回にわたって説明します。

揚力係数、抗力係数

図1.1に示すように、流体中の物体に作用する力のうち、流体との相対速度に垂直な力の成分を揚力、平行な力の成分を抗力と呼びます。 揚力L[N]と抗力D[N]は以下の式で表されます。



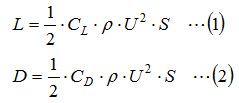
ここで、CLは揚力係数、CDは抗力係数、ρは流体の密度[kg/m³ ]、Uは流体との相対速度[m/s]、Sは翼面積[m² ]です。翼面積は図1.2に示す翼弦長と翼スパンとの積になります。揚力、抗力ともに、流体との相対速度の2乗および翼面積に比例するため、翼の最適設計は、揚力係数が大きく、かつ、抗力係数が小さい翼断面形状を求めることになります。 揚力係数、抗力係数は、風洞実験あるいはCFD解析により求めた揚力、抗力とから、下記の式により求めます。

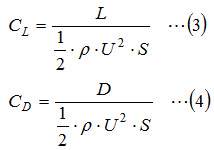
SCRYU/Tetraは、物体表面に垂直に働く圧力成分と水平に働くせん断力を出力しますが、このうち、流れと垂直方向の成分の和が揚力となり、流れと平行な成分の和が抗力となります。

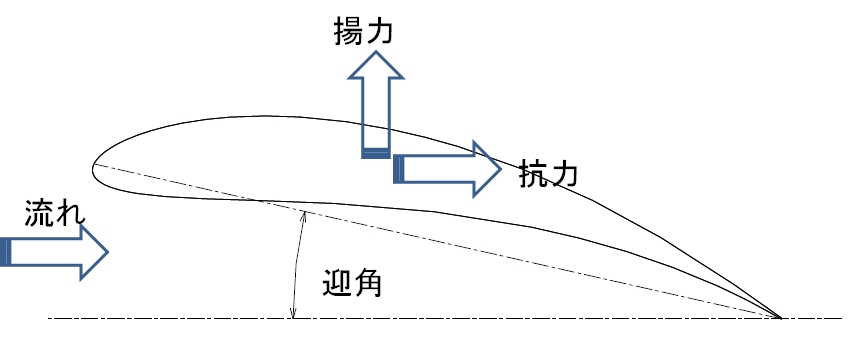
図1.1　揚力と抗力

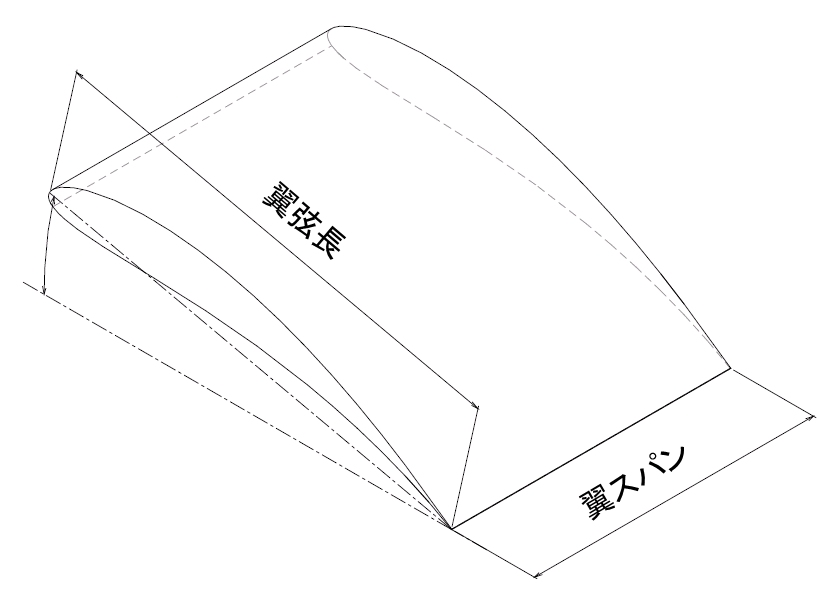
図1.2　翼弦長と翼スパン

風洞実験などにより、揚力係数が大きく、かつ抗力係数が小さくなるような各種の翼断面形状が研究され、図1.3に示すように、迎角を変数としたデータベースとして整えられています。翼の設計は、通常、翼型のデータベースを用いて行いますが、ここでは、任意の断面形状の揚力と抗力をSCRYU/Tetraで数値風洞実験を行うことで求め、EOoptiで揚力係数が最大で抗力係数が最小となるような形状を探索してみます。

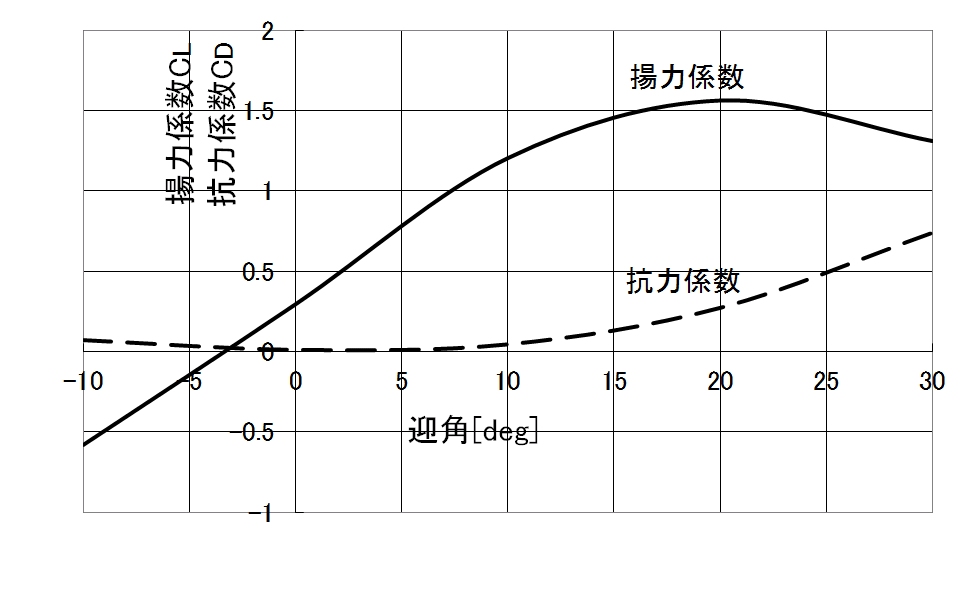
図1.3　迎角による揚力係数と抗力係数の変化

翼断面形状は各種提唱されていますが、モデル作成と解析を容易にするために、2つの変数で形状を定義できるジューコフスキー翼を用いることにします。 ジューコフスキー翼とは、図1.4に示す複素平面ξ-η上の単位円を、下記の式により、図1.5に示すX-Y平面に変換した形状で、ξ-η平面上の円の中心位置を変えることにより、厚みや反りの異なる翼断面形状が得られます。

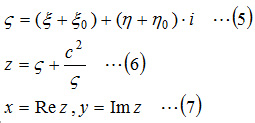
但し、ReZ、ImZはそれぞれZの実数、虚数を表します。
ここで、ｃは図1.4に示す円とξ軸との交点のξ値で、円の中心座標(ξ0,η0)から、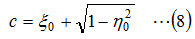として求められます。 図1.6に、各種のξ0とη0の組み合わせでのジューコフスキー翼を示します。ξ0を大きくすると、翼の厚みが増し、また、η0を大きくすると、翼の反りが大きくなることがわかります。

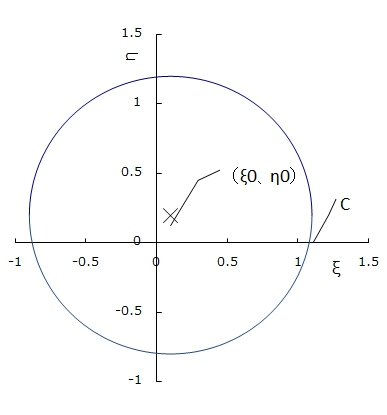
図1.4　ξ-η平面の円

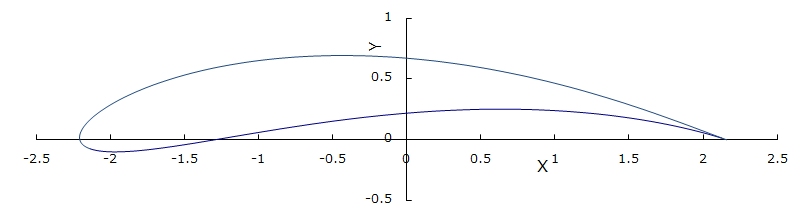
図1.5　ジューコフスキー変換によるX-Y平面への写像

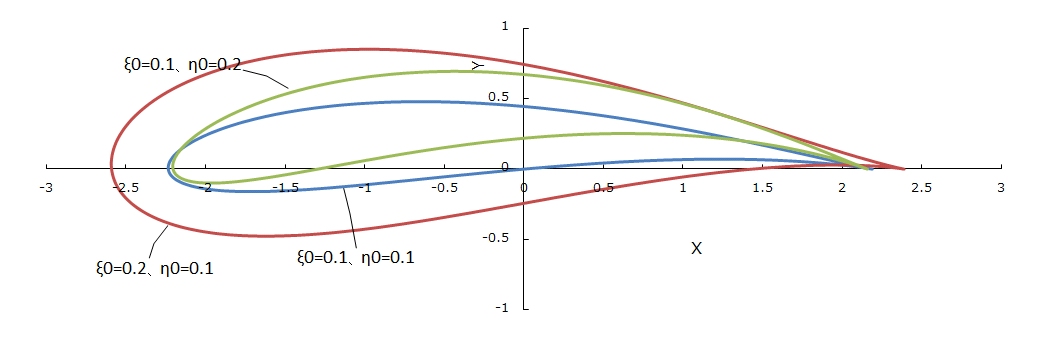
図1.6　ξ0、η0による形状の変化

次回は、モデルの作成について説明します。

【参考文献】 機械工学便覧　流体工学、ユーザーズガイド　最適化編（オプション）

著者プロフィール
御法川 学 氏 | 法政大学 理工学部 機械工学科 教授
環境計量士（騒音・振動） 1992年　法政大学大学院 工学研究科　機械工学専攻

1992年　株式会社荏原総合研究所 入社
1999年　法政大学工学部 助手
2001年　東京工業大学にて学位取得、博士（工学）
2004年　法政大学工学部 助教授
2010年　法政大学理工学部 教授

著者プロフィール
伊藤 孝宏 氏 | オリエンタルモーター株式会社　技術支援部主席研究員

1982年　筑波大学基礎工学類卒業。新日本製鉄株式会社に入社、加熱・冷却設備の開発に従事
1988年　オリエンタルモーター株式会社に入社、送風機の羽根・フレームの開発・設計に従事
2008年　法政大学にて学位取得、博士（工学）
2014年1月現在、オリエンタルモーター株式会社　技術支援部主席研究員

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください