6.5.4 SIMPLE法

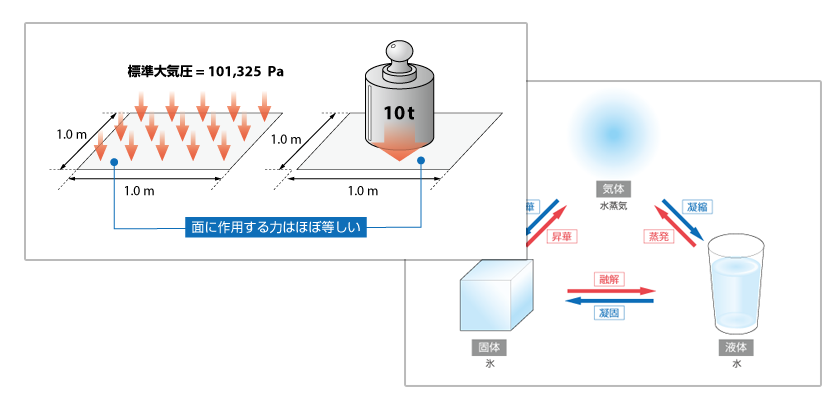
　商用ソフトウェアでは、時間間隔 を大きく取っても、計算を安定に進めやすい SIMPLE法 系統の解法が多く採用されています。実用計算の多くを占める 定常解析 では、擬似的に大きな時間間隔を取って計算を行うため、このことが大きなメリットとなるからです。

　少し難しくなりますが、SIMPLE法で計算を行う場合の手順について、具体的な計算の流れを確認していきたいと思います。なお、以下の式中では 速度 と 圧力 をそれぞれ u と p とします。

1. 現在の圧力を用いて、仮の速度を求める。
   SIMPLE法では 移流項 も 粘性項 も陰的に扱うため、計算式は以下のようになります。

1. 移流項や粘性項に含まれる隣接 要素 の値は仮の速度によって表されるため、上の式は要素数に応じた連立1次方程式となります。これを マトリックス解法 によって解き、仮の速度を求めます。

2. 未来の速度が連続の式を満たすと仮定し、仮の速度に必要な圧力の補正量を求める。
   SIMPLE法では未来の圧力を以下のように考えます。

1. このとき、未来の速度と仮の速度の間には以下の関係が成り立ちます。

1. ここで、未来の速度が 連続の式 を満たす（流体 が湧き出したり吸い込まれたりしない）と考えると以下の式が得られます。

1. 式中の∇をナブラといい、ここでは流体の湧き出しを表す記号だと思ってください。これより圧力を求める以下の式が得られます。

1. この式は圧力に関する連立1次方程式となり、速度と同様にマトリックス解法によって解かれます。

3. 現在の圧力に圧力の補正量を加えて未来の圧力を求める。
   さらに、仮の速度にも圧力の補正量を加味して未来の速度を求める。
   最後に2で得られた圧力の補正量の影響を加味して未来の値を求めます。

1. 以上がSIMPLE法の計算手順となります。また、SIMPLE法から派生した解法にSIMPLEC (SIMPLE-Consistent) 法, SIMPLER (SIMPLE Revised) 法, PISO (Pressure-Implicit with Splitting of Operators) 法などの解法がありますが、これらはいずれも類似した考え方に基づいた解法となります。

 もっと知りたい  　移流項の線形化
　SIMPLE法のように移流項を陰的に扱う場合には、移流項が仮の速度を含んだ表現となるため、素直に定式化することができません。これは移流項が「非線形」であるためです。

　「非線形」という言葉は難しい物理現象の代名詞として用いられている感もありますが、移流項については速度の2乗が含まれていることが「非線形」に当たります。その結果、陰解法 では連立1次方程式を構成することができず、汎用的な数値解法で解くことができません。

連立1次方程式 （未知数どうしの積がない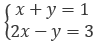）		解ける
連立2次方程式 （未知数どうしの積がある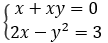）		解けない

　そのため、移流項を陰的に離散化する際には、移流速度として仮の速度の代わりに現在の速度を用いた近似が行われます。現在の値は既知であるため定数として扱うことができ、移流項は線形となるため計算が行える（連立1次方程式を構成できる）というわけです。このように、本来は非線形であるものを何らかの近似によって線形表現にすることを 線形化 といいます。

本来の移流項		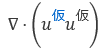非線形 （解けない）
線形化された移流項		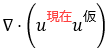線形 （解ける）

　ただし、デメリットがないわけではありません。現在の速度と仮の速度の変化が大きくなると、線形化された移流項は本来の移流項の適切な近似とはなりません。そのような場合には、より細かい時間間隔やサイクル内での繰り返し計算が必要となることがあります。

　なお、移流項を陽的に扱う場合には、現在の値を用いた定式化となるため、このような問題は生じませんが、陽解法に由来した時間間隔の制約が生じることになります。

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。執筆したコラムに「流体解析の基礎講座」がある。　 　

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください