装置設計者のための騒音の基礎 第10回
音響パワー
今回は、音響パワーについて説明します。
音圧は、計測点での音の圧力、すなわち平均圧力からの変化分であるのに対して、音響パワーは、音源から単位時間に放射される音のエネルギー(パワーとは単位時間あたりのエネルギー量)を表します。つまり、音圧が計測する位置により変化するのに対して、音響パワーは計測する位置によらない普遍的な量となります。図1をもとに説明します。音響パワーWは図の音源を囲む閉曲面S上の音響インテンシティIを面積積分した値になります。厳密には、音響インテンシティはベクトルであるため、音響パワーは音響インテンシティと閉曲面の法線ベクトルとの内積の積分になりますが、閉曲面を球体とすると、音響インテンシティの向きと球表面の法線ベクトルの向きとは一致するため、音響インテンシティの大きさを球表面で積分した値と等しくなります。したがって、
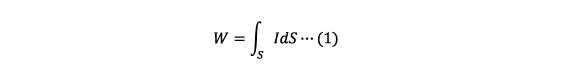
ここで、音響インテンシティIは、音の強さとも呼ばれ、第9回の説明にあるように、音圧pから(2)式で求めることができます。
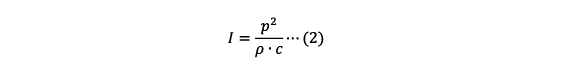
ここで、ρは空気密度、cは音速です。
したがって、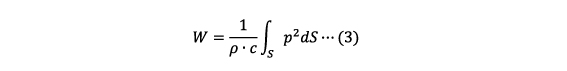
となり、音響パワーは音圧の2乗を、音源を囲む閉曲面上で積分した値に比例します。このことから、音響パワーは音圧の測定結果から求められることがわかります。
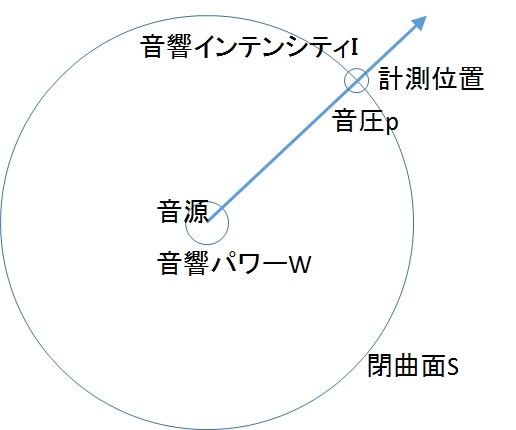
図1 音圧、音響インテンシティと音響パワーとの関係
ここで、閉曲面Sを半径rの球として、音圧pは閉曲面S上では一定値とすると、(3)式は
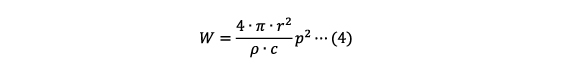
となります。
音響パワーをレベル表現した値が音響パワーレベルLWで、基準値W0=1pW(pピコは10-12を表す接頭辞)との比の常用対数の10倍となります。レベル表現のため、単位はdBです。
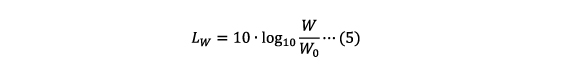
(4)式を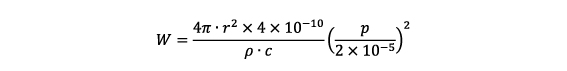
のように変形して、(5)式に代入すると、
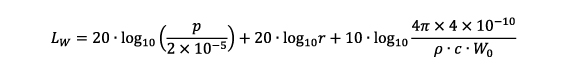
となります。ここで、ρ·c=400、W0=1×10-12 を代入すると第3項は10.99となること、また、第1項は音圧レベルLpであることから、
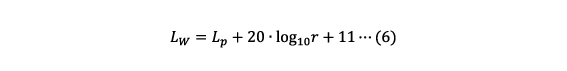
となります。(6)式は、音源から音が球面上に広がる場合の、音圧レベルと音響パワーレベルとの関係を表しています。
では、第8回「音の大きさ」で例として用いた騒音対策前後の音圧レベルから音響パワーレベルを計算してみます。表1に、音源から1mの位置での音圧レベルを示します。計測位置までの距離が1mであるため、(6)式第2項は0となり、音響パワーレベルは、音圧レベルに11を加えたものとなり、対策前の音響パワーレベルは60.4dBで、対策後の音響パワーレベルは53.5dBとなります。
今回は、点音源とみなし、音源を囲む球面上では音圧が一様としたため、音圧レベルは一か所での値で代表していますが、通常は、複数個所での音圧測定が必要となります。詳細は次回説明します。
| 音源から1mでの音圧レベル | 音響パワーレベル | |
|---|---|---|
| 対策前 | 49.4dB | 60.4dB |
| 対策後 | 42.5dB | 53.5dB |
次回は、音響パワーレベルの計測方法について説明します。
【参考文献】 機械音響工学 鈴木ほか コロナ社

著者プロフィール
御法川 学 氏 | 法政大学 理工学部 機械工学科 教授
環境計量士(騒音・振動)
1992年 法政大学大学院 工学研究科 機械工学専攻
1992年 株式会社荏原総合研究所 入社
1999年 法政大学工学部 助手
2001年 東京工業大学にて学位取得、博士(工学)
2004年 法政大学工学部 助教授
2010年 法政大学理工学部 教授

著者プロフィール
伊藤 孝宏 氏 | オリエンタルモーター株式会社 技術支援部主席研究員
1982年 筑波大学基礎工学類卒業。新日本製鉄株式会社に入社、加熱・冷却設備の開発に従事
1988年 オリエンタルモーター株式会社に入社、送風機の羽根・フレームの開発・設計に従事
2008年 法政大学にて学位取得、博士(工学)
2014年1月現在、オリエンタルモーター株式会社 技術支援部主席研究員
最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください


