4.6.4 形態係数

　熱放射 による2面間の 熱移動 を考えるときには、2つの面の位置関係が重要になります。これは面の位置関係によっては、一方の面から放出された熱放射がもう一方の面に届かないためです。例えば、図4.25のように２つの面の間に熱放射を遮蔽する壁がある場合には、2面間での直接の熱放射は起こりません。

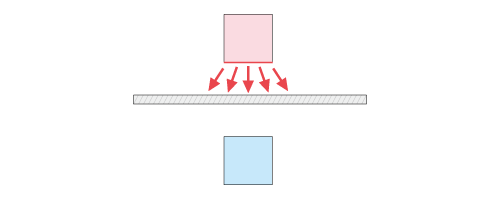
図4.25　熱放射が到達しない例

　この位置関係の影響を表現したものが、2つの面の位置関係や面の大きさ、形状などによって決まる 形態係数 というパラメータです。これは、一方の面からもう一方の面がどのくらい見えるのかを表したもので、0 ～ 1 の値を取ります。例えば、一方の面のあらゆる場所からどの方向を向いたときにももう一方の面が見えるときには、形態係数は1となります。このときにはすべての熱放射が相手の面に到達することになります。逆に一方の面のあらゆる場所からどの方向を向いてももう一方の面が見えない場合には、形態係数は0となります。このような場合には熱放射が相手の面に全く到達しないことになります。

　例として、黒体 が図4.26の位置関係にある場合を考えてみます。面1から面2を見るときには、青線で示すようにどの場所からどの方向を向いても面2が見えることが分かります。そのため、面1から面2への形態係数は1となります。

　一方、面2から面1を見るときには向きによって見え方が異なり、実線で示すように面1が見える場合と破線で示すように面1が見えない場合があります。そのため、面2から面1への形態係数は1より小さな値となります。このように2つの面の関係は、必ずしも相互に同じ値とはならないことに注意してください。

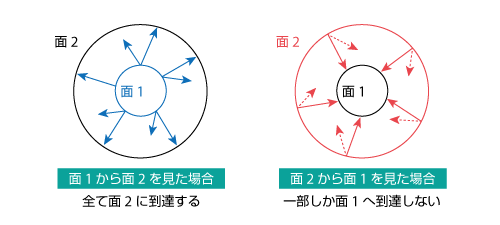
図4.26　形態係数の例

 もっと知りたい  　形態係数と熱放射によって伝わる熱量 

　図4.27に示すような２つの黒体の面の熱放射を考えてみます。

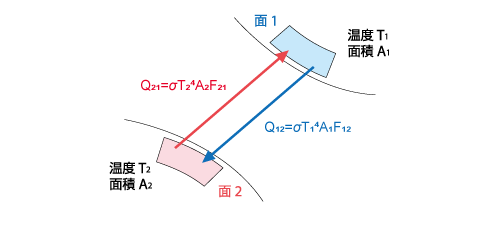
図4.27　2面間の熱放射

　熱放射によって面１から面２へ伝わる正味の 熱量 は、面１が面２に向かって放出したエネルギーと面１が面２から受け取ったエネルギーの差になります。面1から面2を見たときの形態係数を F12、ステファン・ボルツマン定数 を σ とすると、熱量 Q は以下の式で表すことができます。

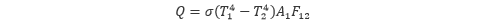
一方、面2から面1を見たときの形態係数を F21として、面2を基準にして考えると、熱量Qは以下の式で表されます。

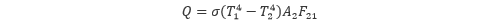
2つの式を見比べると、面の面積と形態係数の間には以下の関係が成り立つことが分かります。

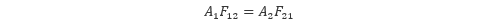
　この例は黒体の場合のものですが、実在する物体では 放射率 が１より小さくなるため、反射 や 透過 を伴うことになります。その場合の熱放射は非常に複雑なものになり、上の式のように面積と形態係数の関係を簡単には表現できなくなります。

---

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。執筆したコラムに「流体解析の基礎講座」がある。　

 

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください