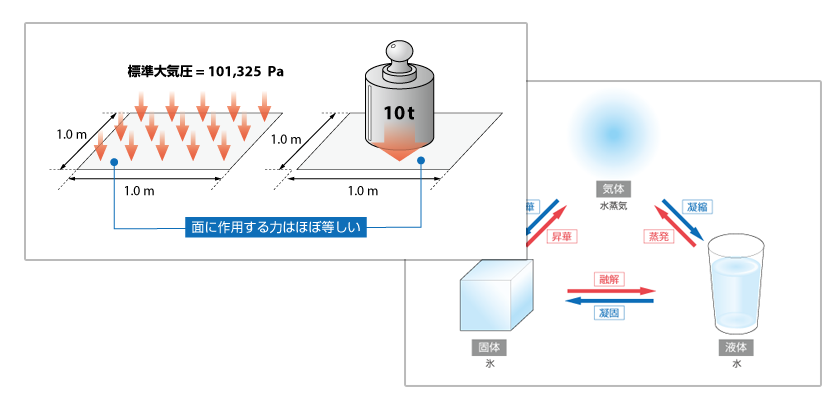
6.5 数値計算法

6.5.1 陽解法と陰解法

　時間の概念がある計算においては、時間の進め方に 陽解法 と 陰解法 という２つの方法があります。陽解法は現在の値のみを用いて、未来の値を予測する方法で、図6.42のようなイメージとなります。

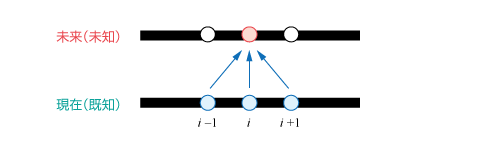
図6.42　陽解法の計算イメージ

　現在と未来を上付き添字、位置を示す i －1 ～ i ＋1 のインデックスを下付き添字で示すと、陽解法で得られる関係式は以下のような形になります。

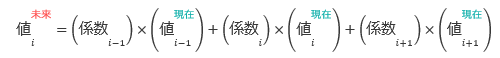
　右辺の 現在 の値はすべて既知であるため、未来 の値は単純な代入操作によって求めることが可能です。そのため、陽解法は1回あたりの計算を高速に行えるとともに、計算プログラムの作成が比較的容易であるという利点を有しています。その反面、計算を安定に進めるためには、時間間隔 を小さく取らなければならず、計算の繰り返し回数が増える分、計算全体に要する時間は長くなってしまうという欠点があります。

　一方で、陰解法は未来の状態に基づく方程式を考えて、解を求める方法です。計算のイメージを示すと図6.43のようになります。

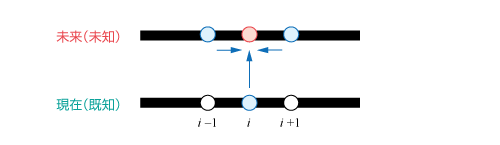
図6.43　陰解法の計算イメージ

　これを式の形で表現すると以下のようになります。

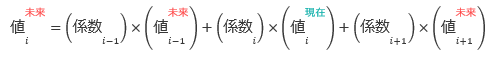
　この計算の時点では 未来 の値は未知数です。したがって、未知数が複数含まれているこの式をこのまま解くことはできません。それでは、どのようにすれば解けるのでしょうか。もう少し具体的に見ていきたいと思います。

　例として、図6.44に示すように1次元の領域を5分割し、左から順に1, 2, 3, 4, 5と番号をつけて考えます。

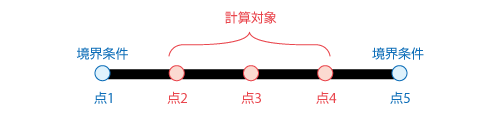
図6.44　5分割された1次元領域

　両端の点1と点5は 境界条件 によって値が定まるため、実質的な計算対象は点2 ～ 4です。先ほどと同じ要領でそれぞれの点における式を考えると、以下の3つの式が得られます。

　前述の通り、点1と5の値は境界条件で決まるため既知です。したがって、未知数は点2 ～ 4の値となりますが、未知数3つに対して方程式が3つあることから、この連立方程式を解くことができれば未来の値を求められることがわかります。

　この例では計算点が3つなので、3元連立1次方程式となりましたが、実際には要素数と解かれる変数の数に応じて連立方程式が作られます。例えば、3次元の 流れ と 温度 の計算を要素数100万で行うとすると、100万元連立1次方程式が5つ（速度 のX成分, Y成分, Z成分, 圧力, 温度）作られることになります。

　このように、陰解法では連立1次方程式を解く必要があり、陽解法に比べて計算手順が煩雑になります。そのため、１回あたりの計算時間が長くなるとともに、計算プログラムも複雑なものになります。その反面、陽解法と比較してより大きな時間間隔で計算を行うことが可能です。これによって、計算の繰り返し回数が少なくなり、計算全体に要する時間が短くて済むという利点があります。

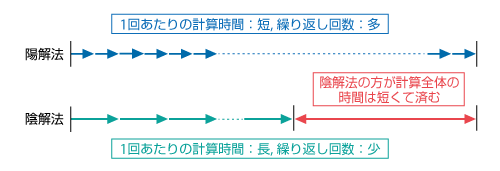
図6.45　陽解法と陰解法の比較

　実用計算では、時間間隔をできるだけ大きく取って計算時間を短くしたいという要求が強いことから、多くの商用ソフトでは陰解法が採用されています。

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。執筆したコラムに「流体解析の基礎講座」がある。　

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください