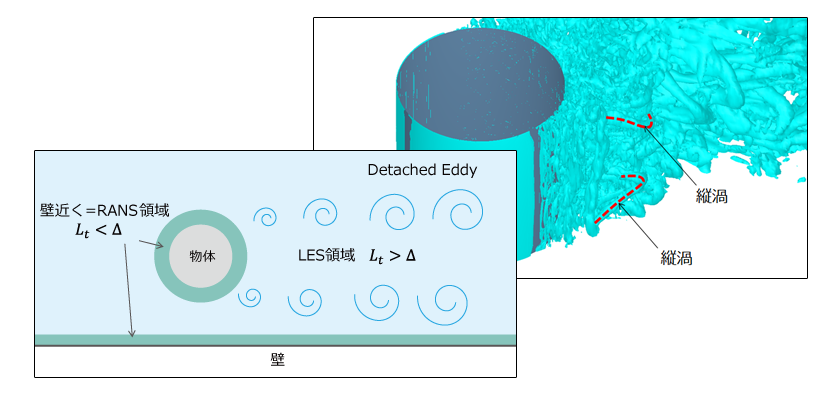
層流と乱流の判断

18.1　レイノルズ数の見積もり

　これまで 乱流 について、メカニズムと計算方法などをご説明してきましが、今回は 層流 で解析するか、乱流で解析するかの判断で用いる レイノルズ数 の見積もりについてご説明します。レイノルズ数Reは、

Re＝（流体の密度×代表速度×代表長さ/流体の粘性係数）

という式で計算し、流体の慣性力と粘性力の比であるとも説明されます。 密度 と 粘性係数 は 流体 の種類で決まるものですので議論の余地はないと思います。一方、「 代表速度 」と「 代表長さ 」は、対象とする流れ場の状況に依存する値ですので、どのように見積もるかは頭を悩ませるところです。ここでの「代表」とは計算しようとする（注目する）流れ場を特徴づけるもの、とご理解いただくと良いと思います。
代表速度と代表長さの取り方について例を示します。図18.1のようなボール周りの流れ場を考えると、流入速度Uが代表速度、ボールの大きさ（直径）Dが代表長さとなります。もし、ボールがゴルフボールで、そのディンプルひとつだけを取り出して詳細に計算しようとする場合には、図18.2のように代表長さはディンプルの深さや直径となります。

図18.1　ボール周り流れの代表速度と代表長さ

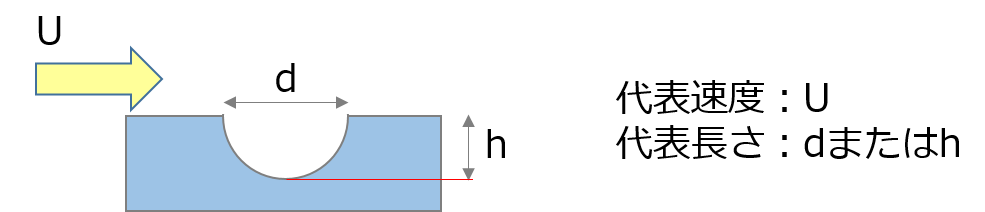
図18.2　ディンプル周り流れの代表速度と代表長さ

　図18.3のようにサイズの異なる物体が 流れ の中にあるときは、代表長さの選択に迷われると思いますが、その中で最も長いものを代表長さとするのが良くとられる方法です。しかし、レイノルズ数はオーダーが見積もれれば十分ですので、物体のサイズに大きな違いがなければ、複数の選択肢のうちのどれを使っても良いとも言えます。

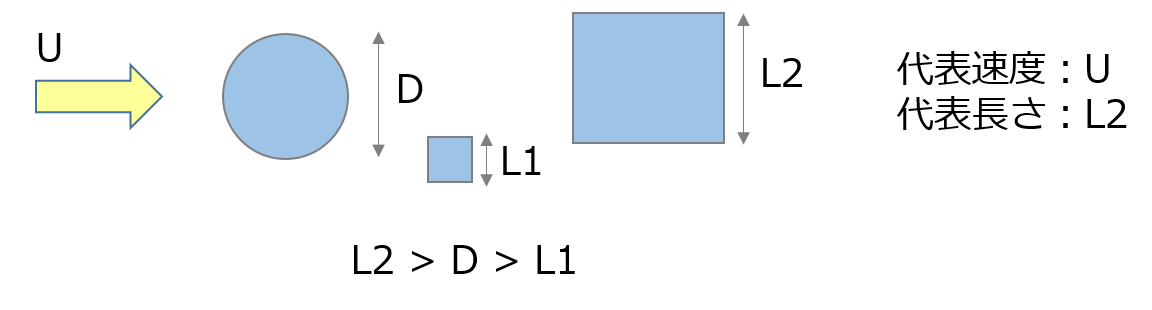
図18.3　複数の物体が存在する流れ場の代表長さ

　もうひとつ例を示します。図18.4のように管の中に物体が置かれている状況の 流れ解析 です。代表長さの選択肢としては、物体の高さhと管の直径Dがあります。物体周りにのみ注目する場合は物体の高さhで良いかと言えば、物体の上流側の流れ場を特徴づけるのは管の直径Dということを考えると、代表長さはDということになります。

図18.4　内部流における代表長さ

　レイノルズ数の見積もりを4つの例でご説明しました。結局、絶対的な指針はなく、曖昧さが残るのがレイノルズ数の見積もりですが、これらの例からレイノルズ数の見積もり方のイメージを掴んでいただけましたら幸いです。次回は身近な現象の計算例(2)をご紹介します。

著者プロフィール
伊丹 隆夫 | 1973年7月 神奈川県出身
東京工業大学 大学院 理工学研究科卒業
博士（工学）

大学では一貫して乱流の数値計算による研究に従事。 車両メーカーでの設計経験を経た後、大学院博士課程において圧縮性乱流とLES(Large Eddy Simulation)の研究で学位を取得し、現職に至る。 大学での研究経験とメーカーの設計現場においてCAEを活用する立場という2つの経験を生かし、お客様の問題を解決するためのコンサルティングエンジニアとして活動中。

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください