パッと知りたい! 人と差がつく乱流と乱流モデル講座 第13回 13.1 円柱周り流れ解析、13.2 LESの計算結果、13.3 RANSとの比較
乱流の計算方法 (7) LESの計算例
13.1 円柱周り流れ解析
前回は LES の概要をお話ししました。今回は具体的な計算例をご紹介します。「第5回 乱流のメカニズム(2) 」でアニメーションのみご紹介した円柱周り流れの計算例です。円柱周り流れとは、図13.1のように一様な 速度 を持つ 流れ の中に配置された円柱の周りに発生する流れの現象を計算するものです。流れが円柱を過ぎるとき、有名な「 カルマン渦 」と呼ばれる 渦 が発生しますが、円柱にぶつかる流れの 速さ 、 流体 の種類( 密度 、 粘性 )、円柱の直径の関係によって、カルマン渦が発生しない場合やカルマン渦よりも複雑な渦構造が出現する場合もあります。今回、ご紹介する計算例は円柱の直径と流れの速さに基づくレイノルズ数が1000万という非常に高いレイノルズ数の円柱周りの流れで、非常に複雑な渦構造が円柱の周りに出現します。 レイノルズ数 1000万という条件は、時速200km/hで走行する新幹線の周りの空気の流れに相当します。
図13.1 円柱周り流れの計算
13.2 LESの計算結果
図13.2はLESによる円柱周り流れの 渦管 を 速度勾配テンソルの第2不変量 で可視化した図です。

図13.2 円柱周り流れの計算結果(LES)
速度勾配テンソルの第2不変量とは、
(渦度の大きさ - せん断の大きさ)
を表す指標で、それが正の値、つまり 渦度 がせん断より強い領域を描くと図13.2のように渦管を可視化することができます。この計算では円柱後方の領域に多数の細かい渦管が発生しているのが分ります。その細かな渦管は下流に進むにしたがって、徐々に大きな渦管へと変化していますが、同時に渦管の塊自体が大きく蛇行している様子も見えます。細かい渦管の発生と、大きな運動としてのカルマン渦の発生が重なり合っているような状況です。
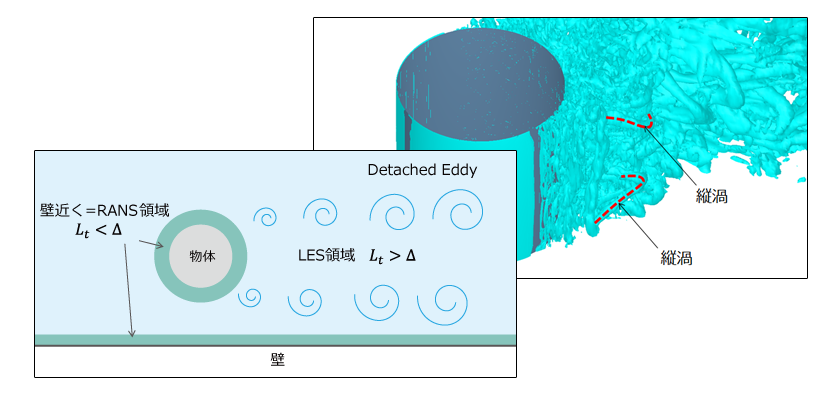
ところでカルマン渦は円柱と平行、つまり流れに対して垂直に発生する渦管ですが、図13.2の渦管を良く見てみると、カルマン渦の方向と異なる方向に向いている渦管が発生していることが分ります(図13.3)。これは「縦渦」と呼ばれる渦管で、 乱流 による運動が活発になると出現する渦管です。方向の異なる渦管がお互いに干渉すると、加速度的に複雑な渦構造が形成されると言われています。
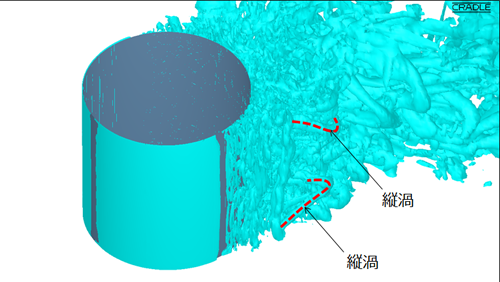
図13.3 円柱付近の拡大図(LES)
LESで必要なメッシュが準備できれば、このような複雑な渦管の運動を捉えることができるのが分ります。人間の社会も少し異なる人が混じると、その組織は活性化すると言われます。乱流も人の社会も同じようなメカニズムであることが興味深いところです。
13.3 RANSとの比較
図13.4は RANS を用いて、同じ メッシュ と条件で円柱周り流れの計算を行った結果です。乱流モデルにはSST k-ωモデルを用いています。図13.2と比較して、渦管の様子が全く違うことにお気づきになると思います。RANSの計算では円柱と平行で、かつ太い渦管が形成されているだけで、縦渦も細かい渦管も認められません。また、円柱後方で渦管が蛇行する様子はなく、ほぼ直進しています。RANSではいくら細かいメッシュを配置しても、円柱表面における非定常性の強い細かい渦管の発生が予測できず、その後の複雑な渦構造の発達に至らないためと考えられます。

図13.4 円柱周り流れの計算結果(RANS)
図13.5は 渦粘性係数 をLESとRANSで比較した図です。LES、RANSとも渦管の周りに渦粘性係数が大きい領域が見られますが、RANSではLESと比べて非常に大きな渦粘性係数を予測しています。この大きな渦粘性係数のために、RANSでは細かい渦管の生成が抑制されていると考えられます。次回はLESとRANSを組み合わせた「 ハイブリッドモデル 」についてお話しします。
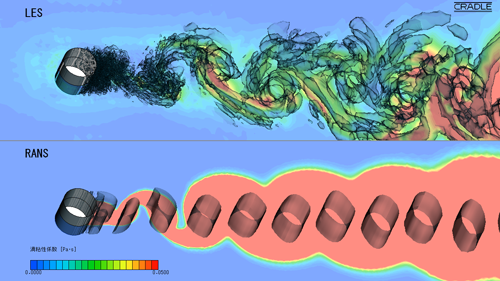
図13.5 渦粘性係数分布の比較

著者プロフィール
伊丹 隆夫 | 1973年7月 神奈川県出身
東京工業大学 大学院 理工学研究科卒業
博士(工学)
大学では一貫して乱流の数値計算による研究に従事。 車両メーカーでの設計経験を経た後、大学院博士課程において圧縮性乱流とLES(Large Eddy Simulation)の研究で学位を取得し、現職に至る。 大学での研究経験とメーカーの設計現場においてCAEを活用する立場という2つの経験を生かし、お客様の問題を解決するためのコンサルティングエンジニアとして活動中。
最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください


