コラム:乱流
新しい順 | 古い順


パッと知りたい! 人と差がつく乱流と乱流モデル講座 第18回 18.1 レイノルズ数の見積もり

パッと知りたい! 人と差がつく乱流と乱流モデル講座 第17回 17.1 ディンプルの影響

パッと知りたい! 人と差がつく乱流と乱流モデル講座 第16回 16.1 ゴルフボールの流れ 解析概要、16.2 ゴルフボールの流れ 解析結果

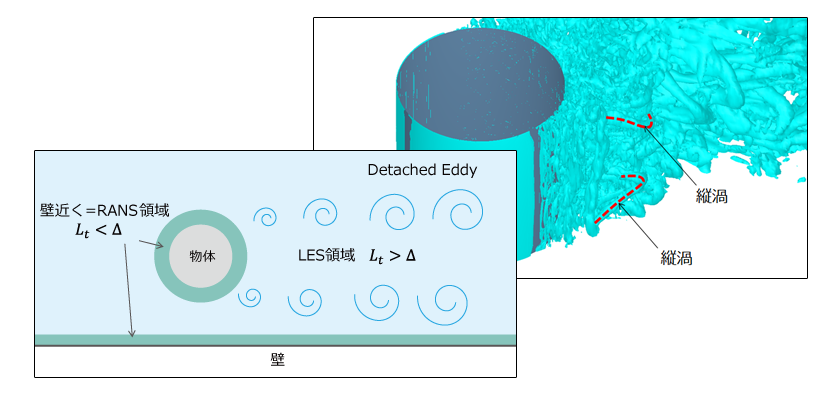
パッと知りたい! 人と差がつく乱流と乱流モデル講座 第15回 15.1 DESによる円柱周り流れの計算例

パッと知りたい! 人と差がつく乱流と乱流モデル講座 第14回 14.1 ハイブリッドモデル概要、14.2 DES、14.3 VLES

パッと知りたい! 人と差がつく乱流と乱流モデル講座 第13回 13.1 円柱周り流れ解析、13.2 LESの計算結果、13.3 RANSとの比較

パッと知りたい! 人と差がつく乱流と乱流モデル講座 第12回 12.1 Large Eddy Simulation、12.2 Smagorinskyモデル、12.3 スケール相似則モデル

パッと知りたい! 人と差がつく乱流と乱流モデル講座 第11回 11.1 バックステップ流れ、11.2 翼周り流れ



