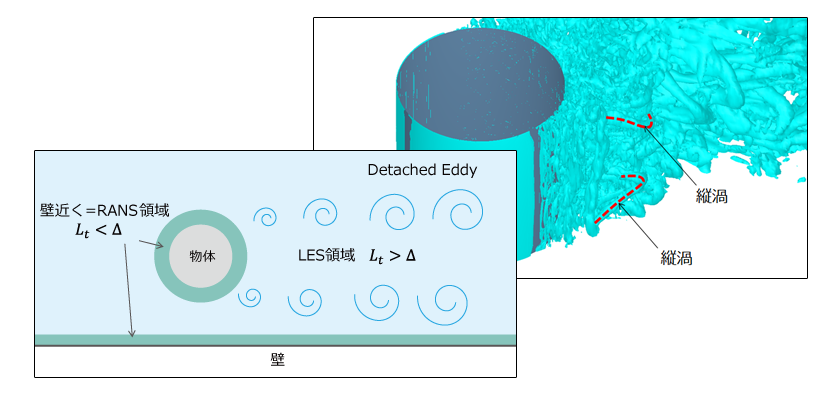
乱流の計算方法 (4) レイノルズ平均モデル RANSの壁条件

10.1　RANSの壁条件

　 RANS では平均の流れ場を計算することを目的にし、それに対する非定常的な渦運動の効果を渦粘性として計算に取り込んでいることをお話してきましたが、RANSに関するもうひとつの重要な話として壁の扱いがあります。今回はRANSにおける壁条件についてお話しします。

　壁の上では流れは止まっていますが、壁から離れるに従って流れは速くなっていきます。それは川の 流れ をイメージしていただくと分り易いと思います。岸の近くの流れより、岸から離れたところの流れの方が速い（危険）というイメージがありますよね。そのような壁からの距離に従った流れの速さの変化が、 乱流 では急になります。なぜ、変化が急になるのかは、流れの勢いがある（慣性が大きい）ため、壁際のぎりぎりまで流れが速いというようにイメージしていただけば良いと思います。流れの計算をする際には、その変化を正確に捉える必要がありますが、 流速 の変化の起きる距離は流れ場全体の大きさから見ると非常に短いため、その距離に合わせ メッシュ を配置しようとすると、膨大な計算規模になる恐れがあります（図10.1）。そこで、壁近傍のメッシュを厚めにして計算できる工夫が必要とされます。

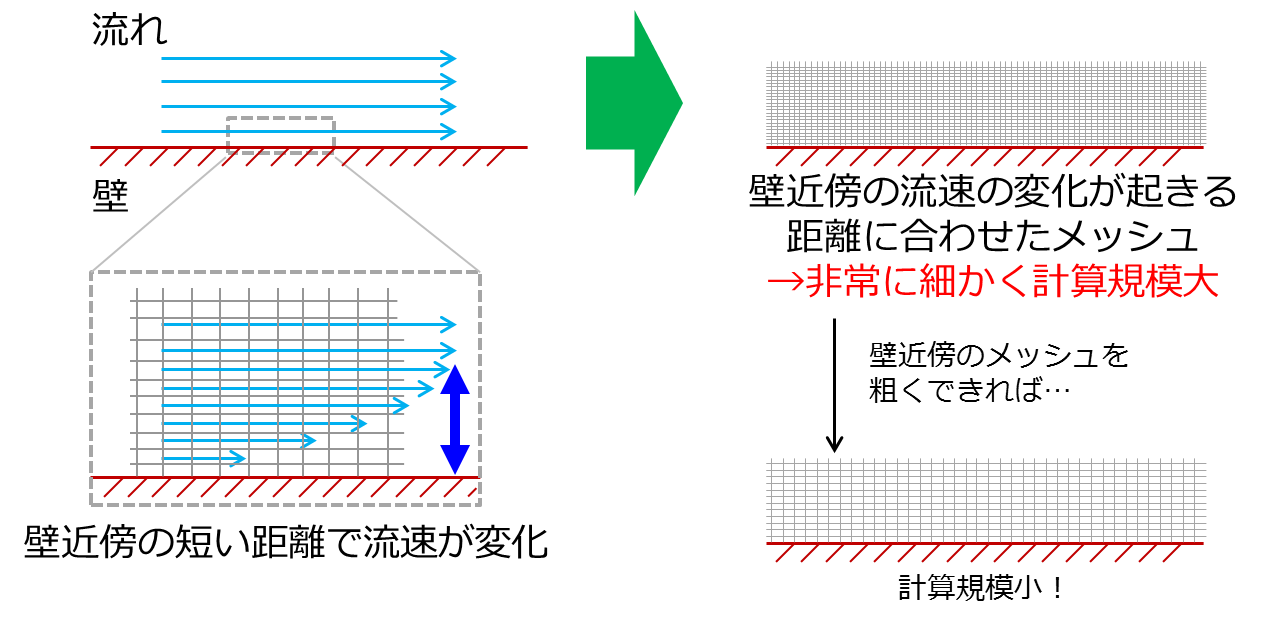
図10.1　壁近傍のメッシュと計算規模

10.2　壁関数

　壁近傍のメッシュを厚くして計算するための工夫は、いわゆる「 壁関数 」というものです。壁関数として良く用いられるものが「 対数則 」です。対数則とは、図10.2の右半分のグラフのように壁からの距離と、そこでの流速の大きさを横軸対数で表示したときに直線になる分布です。図中の y+ とu+は、それぞれ壁面上の 摩擦速度 （摩擦の大きさ）で無次元化した壁からの距離と流速です。この無次元化により、 流体 の種類や流速が異なっても、同じカーブの上に乗るようになります。対数部分よりも壁側には「 粘性底層 」と「 緩和層 」と呼ばれる領域があり、対数の部分は「 対数領域 」と呼ばれます。粘性底層では狭い範囲で急激に流速が増加し、緩和層で対数則分布へと移行します。このように乱流状態における壁近傍の流速の変化は複雑なのですが、粘性底層まで含めてメッシュで捉えようとすると、前述のようにかなり細かい間隔でメッシュを配置する必要があります。そこで、対数則を壁条件として用いると、粘性底層から緩和層にかけてのメッシュ配置を省略することができ、壁に配置するメッシュを厚くすることが可能になります。

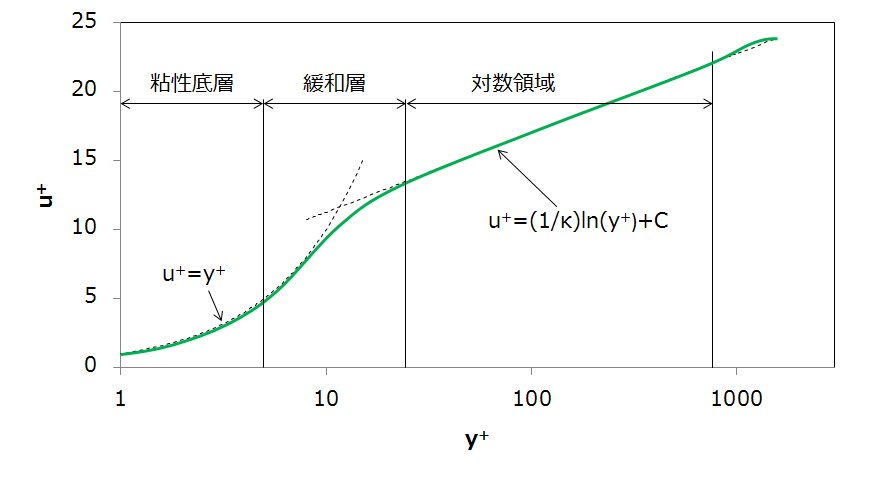
図10.2　対数則速度分布

　対数則条件を生かすには、流速が対数に乗る「対数領域」にメッシュの第1点を配置する必要があります。より細かく配置すれば良いだろうということで、中途半端に粘性底層や緩和層にメッシュの第1点が配置されると、壁条件に対数則条件が適用できず、逆に精度の悪い計算になります。一般にメッシュは細かくて悪いことはないのですが、乱流計算における壁近傍のメッシュは少し事情が違います。壁関数を用いるときには、壁上のメッシュ高さに注意を払う必要があります。

10.3　乱流モデルと壁条件

　対数則は理論と実験を組み合わせて得られた式ですが、図10.3の左側のように流れが壁に沿う単純な流れ場でのみ成立する条件です。図10.3の右側のように壁面に凹凸があると、対数則が成立しない部分が生まれます。そのようなケースでは、対数則を使わず粘性底層や緩和層の中にも複数のメッシュを配置して計算する必要がありますが、そのときに適用する乱流モデルに注意が必要です。壁近傍では壁によって渦運動が拘束されますので、壁から離れた領域の渦運動とは状況が異なり、通常の乱流モデルの前提が崩れるからです。壁近傍での使用にも対応している乱流モデルが、「低レイノルズ数型」と呼ばれる乱流モデルです。ここでの「 低レイノルズ数 」とは、壁近くの流れが遅い領域という意味で、流れ場自体が低いレイノルズ数のときに適用するモデルという意味ではありません。代表例としては、「安倍・近藤・長野モデル(AKNモデル)」、「SST k-ωモデル」などがあります。
　なお、低レイノルズ数型モデルは、壁から離れると通常の乱流モデルと等価になる式になっています。そのため、全部の壁において薄いメッシュを配置する必要はなく、対数則が成立しない領域や、壁際の現象を解析したい注目領域だけを薄いメッシュとすることで、壁面近傍の精度を保つことができます。次回もRANSの続きをお話しする予定です。

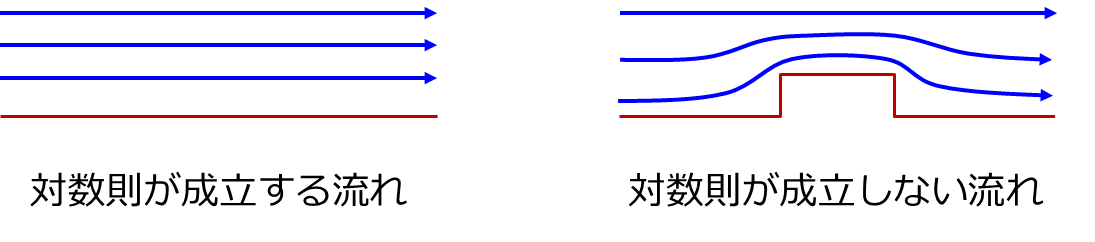
図10.3　対数則と流れの関係

著者プロフィール
伊丹 隆夫 | 1973年7月 神奈川県出身
東京工業大学 大学院 理工学研究科卒業
博士（工学）

大学では一貫して乱流の数値計算による研究に従事。 車両メーカーでの設計経験を経た後、大学院博士課程において圧縮性乱流とLES(Large Eddy Simulation)の研究で学位を取得し、現職に至る。 大学での研究経験とメーカーの設計現場においてCAEを活用する立場という2つの経験を生かし、お客様の問題を解決するためのコンサルティングエンジニアとして活動中。

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください