もっと知りたい！熱流体解析の基礎61　第6章熱流体解析の手法：6.5.2 マトリックスソルバー (1)

2019/04/25

6.5 数値計算法

6.5.2 マトリックスソルバー (1)

　前回述べたように陰解法では、要素数に応じて連立方程式が作られます。前回と少し表現を変えていますが、このときの各要素に関する方程式は、図6.46に示すように隣接する要素の値を含んだ表現となります。

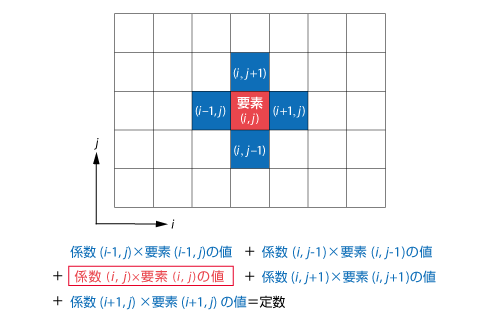
図6.46　各要素に関する方程式の一般形

　ここでは、2次元の直交格子を例に取りましたが、3次元であれば奥行き方向も含まれるため、手前側と奥側の要素を含めた7項の方程式になります。また、非構造格子で隣接する要素がさらに多い場合にはより多くの項が含まれることになります。なお、右辺にある定数は外部からの作用を表したもので、流れであれば外力、温度であれば発熱や吸熱がある場合に値が入ります。

　ところで、連立方程式は行列を用いて表現することが可能です。例として、式(1)の連立方程式を考えます。

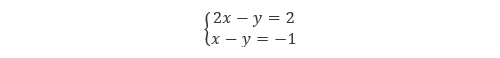(1)

　これを行列形式で表現すると、式(2)のようになります。

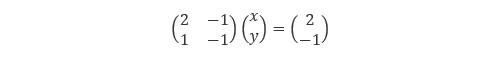(2)

　各要素について考えられた連立1次方程式も、上述のように行列形式で表現することができます。一方で、行列のことを英語でmatrix（マトリックス）ということから、大規模な連立一次方程式を解く手法のことをマトリックス解法やマトリックスソルバーと呼ぶ場合があります。マトリックス解法は直接法と反復法に大別されますが、方程式系の規模や性質から、熱流体解析では通常、反復法が用いられます。

　それでは、先ほどの2元連立1次方程式を、最も基本的な反復法であるヤコビ法によって解く手順を見ていきたいと思います。なお、連立方程式の解析解は x = 3, y = 4 です。まず、以降の計算をわかりやすくするために、式(1)を以下のように変形します。

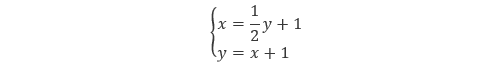(3)

　計算を行うために適当な初期値を設定します。ここでは x と y の初期値をともに 0 として、式(3)の右辺に代入します。

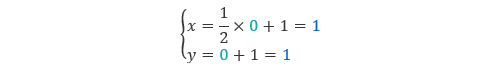(4)

　これによって、1回目の解はx = 1, y = 1 と求められます。次にこの x と y の値を再び元の式(3)に代入します。

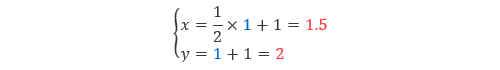(4)

　そうすると、2回目の解としてx = 1.5, y = 2 が得られ、1回目よりも解析解に近づいていることがわかります。この操作を繰り返していくと表6.2に示す結果が得られます。

表6.2　ヤコビ法による計算結果

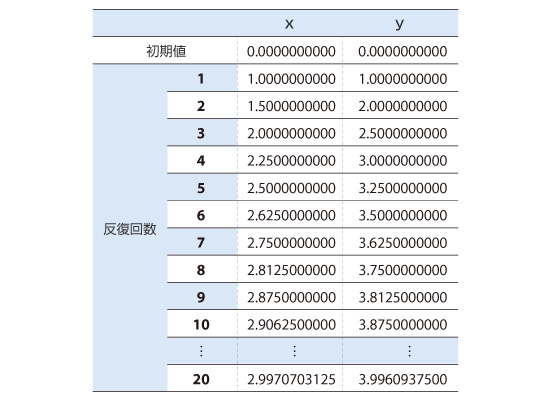
　計算の繰り返し回数のことを反復回数やイタレーション回数といいますが、反復回数が増えるにつれて、x と y の値が解析解に近づいていることがわかります。ここでは説明を簡単にするためにヤコビ法を例に取りましたが、実際にはより少ない反復回数で解が得られる反復法が用いられます。

もっと知りたい 係数行列
　以下の連立1次方程式を考えます。

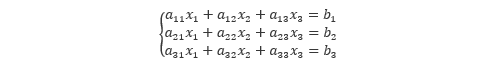
　これを行列形式で表現すると、以下のようになります。

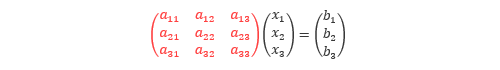
　上式において赤字で示した行列は各項の係数が集められたもので、これを係数行列といいます。熱流体解析の係数行列は、計算対象の要素とそれに隣接する要素の係数のみが0以外の値となり、その他の大半の係数は0となります。

　例えば、100万要素の3次元直交格子を考えたとすると、係数行列のサイズは100万行×100万列となりますが、各行で0以外の値となるのは7個の成分のみです。このように大半の成分が0となる行列のことを疎行列やスパース行列といい、一般にはこの特性を活用した、省メモリかつ高速に計算可能な反復法が用いられています。

もっと知りたい 直接法
　熱流体解析で直接法が用いられることはほとんどありませんが、ここでは参考までに式(2)の連立1次方程式を最も基本的な直接法であるガウスの消去法によって解く手順を見ていきます。

　1. 2行目から1行目×1/2を引きます。

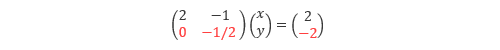
　2. 2行目の y の係数が1になるように2行目に－2を掛けます。

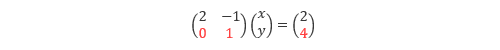
　これで y の値が求まりました。ここまでの一連の操作を前進消去といいます。

　3. 1行目に2行目の値を加えます。

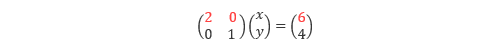
　4. 1行目の x の係数が1になるように1行目に1/2を掛けます。

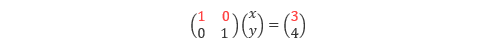
　ここまでの操作を後退代入といいます。これで x の値も求まり、連立方程式が解けたことになります。計算の手順としては、前進消去によって係数行列の下三角成分を0にしたあと、後退代入によって上三角成分を０にするという流れになります。直接法は反復法よりも計算量が多くなる反面、コンピューターの計算誤差の範囲内で厳密な解を得ることが可能で、構造解析のなどの分野で用いられています。

著者プロフィール
上山篤史 | 1983年9月兵庫県生まれ
大阪大学大学院工学研究科機械工学専攻博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。執筆したコラムに「流体解析の基礎講座」がある。　