6.5.8 移流スキームと数値拡散

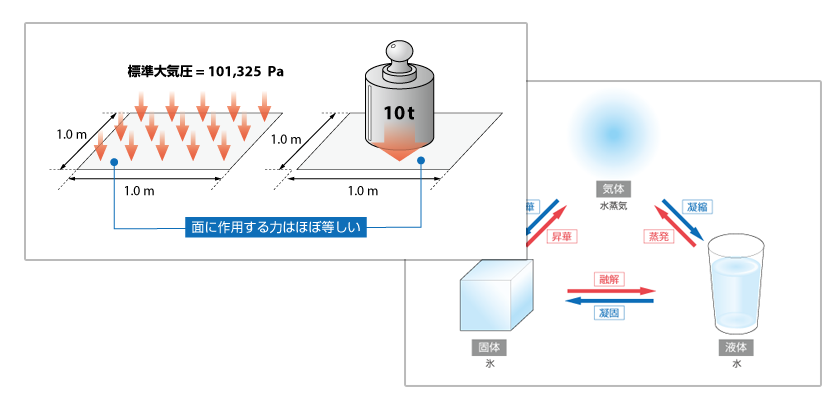
　ナビエ・ストークス方程式 などに見られる 移流項 は、上流から 流れ によって情報が運ばれてくる効果を示した項です。煙突から出た煙が風上には伝わらないように、移流項のモデル化には流れの向きを考慮するのが自然であり、そのため移流項に対しては特有の 離散化 が行われます。これらの手法を総称して 移流スキーム といいます。

　移流スキームにはいくつかの方法がありますが、代表的なものとして 風上差分（または 上流差分）があります。これは計算点の上流の情報を参照する方法で、流れの向きによって参照する 節点（要素）が変わります。これを示したものが図6.54です。

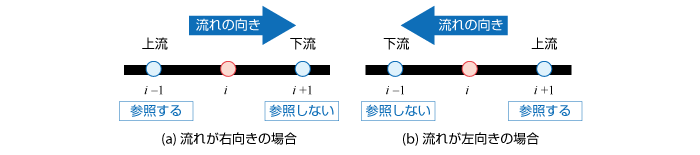
図6.54　流れの向きと参照点の関係

　点の間の距離を Δx とすると、風上差分の式は以下のようになります。第49回 と同様の方法で誤差評価を行うと1次精度となることから、このスキームは 1次精度風上差分 と呼ばれます。

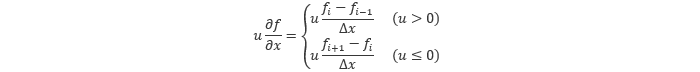
　風上差分特有の性質に 数値拡散 があります。これは、風上差分を用いたときに生じる人工的な拡散作用で、計算を安定にするメリットがある反面、メッシュ 斜め方向への流れがある場合に鈍った解が得られてしまうというデメリットがあります。また、数値拡散の及ぼす影響はメッシュの細かさや移流スキームの精度によって異なります。それを示したものが図6.55です。

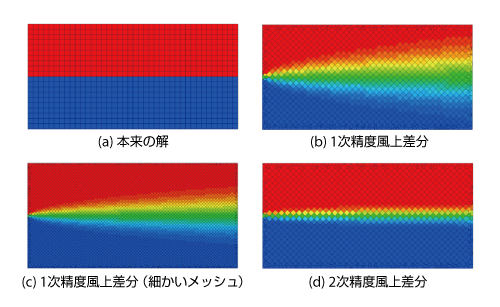
図6.55　移流スキームやメッシュサイズによる違い

　細かい計算条件は割愛しますが、流れは図中の右向きであり、(a)に示すように青と赤が明確に分離するのが本来の解になります。風上差分を用いても、(a)のように流れがメッシュに沿う場合には数値拡散の影響は見られません。

　一方、流れに対してメッシュが傾いていると数値拡散の影響が現れます。(b)は1次精度風上差分を用いたものですが、青と赤の境界面がぼやけている、すなわち、鈍った解が得られていることが分かります。ただし、(c)のように同じ1次精度風上差分でもメッシュを細かくするとぼやけ方が軽減されます。また、(d)の2次精度風上差分のように高次精度のスキームを用いると、同じメッシュサイズであっても同様にぼやけ方を軽減することができます。

　この結果を見ると、メッシュが細かく、高次精度のスキームであるほど色が変化する範囲が狭くなっており、シャープな解が得られていることが分かります。ただし、数値拡散が少ないほど計算は不安定になりやすくなるため、計算の状況に応じて解法を選択することが必要といえます。

 もっと知りたい  　数値粘性
　1次元の 移流拡散方程式 を例に取り、数値拡散について具体的に見ていきます。

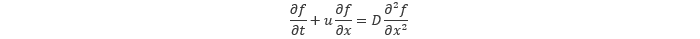
　ここでD は 拡散係数 です。移流速度u を正の値として、上式の移流項を1次精度風上差分で離散化してみます。

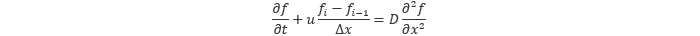
　風上差分に伴う誤差を確認するため、上式の風上差分に対して テイラー展開 を用いて、誤差の第1項までを含めた表現に書き換えると以下のようになります。

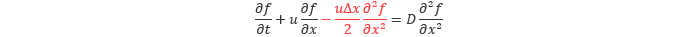
　上式の赤字の部分が風上差分に伴う主要な誤差です。この式を変形して以下のように書き換えます。

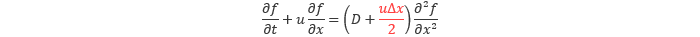
　そうすると赤字の分だけ 拡散項 の係数が増えていることがわかります。これによって、本来よりも拡散的、すなわち鈍った解が得られてしまいます。流れの場合には、拡散係数は 粘性係数（分子粘性）を表すことから、ナビエ・ストークス方程式における数値拡散は 数値粘性 とも呼ばれます。

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。執筆したコラムに「流体解析の基礎講座」がある。　 　

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください