3.5 流れの性質

3.5.1 ベルヌーイの定理

　図3.33に示すように水平な円管を流れる 理想流体 の 定常流れ を考えます。理想流体とは 粘性 がない 非圧縮性流体 のことで、粘性がないため摩擦による損失はありません。 流れ の位置エネルギーが変化しないものとすると、流れが持つエネルギーは、流れの運動エネルギーと 圧力 のエネルギーとなります。

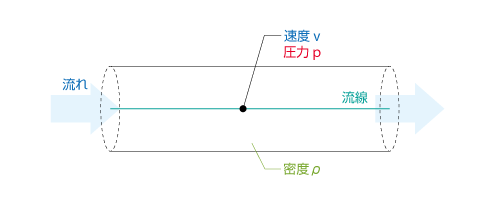
図3.33　流れのエネルギー

　単位体積あたりの流れの運動エネルギーは 流体 の 密度 を ρ [kg/m³ ]、 速度 を v [m/s] とすると ρv²/2 [Pa] で与えられ、その単位は圧力と等しくなります。単位体積あたりで考えていますが、これは質量 m [kg] の物体の場合に、mv²/2 の形で与えられる運動エネルギーと同じものです。一方、圧力のエネルギーとは圧力 p [Pa] そのもののことです。 流線 上では、これらのエネルギーの和が保存されるため、次の式が成立します。

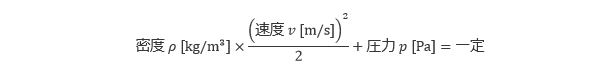
　これを ベルヌーイの定理 といいます。このうち、運動エネルギーのことを 動圧 、圧力のことを 静圧 といい、これらの和を 全圧 または 総圧 といいます。ベルヌーイの定理は動圧と静圧の和が一定となることを示しており、速度が速くなると圧力が下がり、逆に速度が遅くなると圧力が高くなることを表しています。例えば、図3.34のように断面積が変化する管では、断面1よりも断面2のほうが、速度が速い分、静圧（圧力）は低くなります。

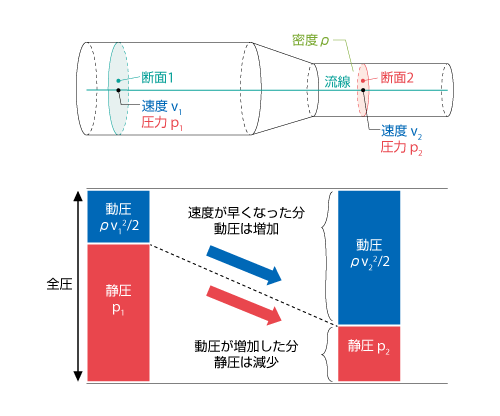
図3.34　断面積が変化する管

　また、位置の変化が無視できない場合には、これに加えて位置エネルギーを考える必要があります。位置エネルギーは密度 ρ [kg/m³] と 重力加速度 g [m/s²]、基準位置からの高さ z [m] の積で表されます。これを含めると、先ほどの式は以下のように書き換えられます。

　図3.35に示すように側面に小さな穴が開いた水槽を考えます。穴の大きさに対して水槽の断面積は十分大きく、水面の速度は0と見なせるものとします。点1と点2の圧力がともに大気圧で等しいとすると、ベルヌーイの定理から位置エネルギーが変化した分だけ動圧が増加し、水が流れ出るということが分かります。

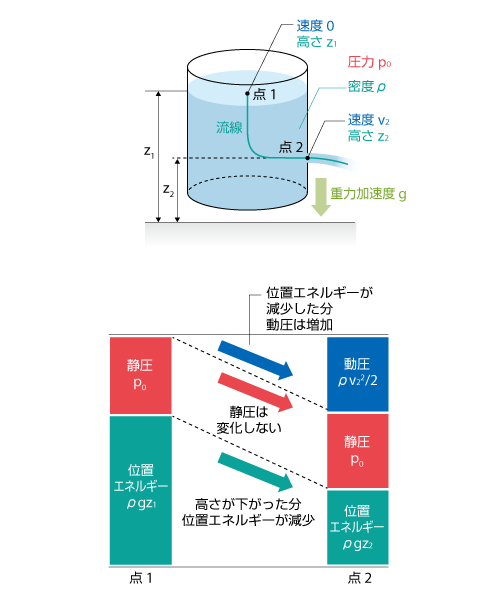
図3.35　水槽から流れ出る水

なお、先ほどの式の各項を密度と重力加速度で割った、次の表現が用いられる場合もあります。

　上式の各項の単位は m となり、各項のことを左辺の第1項から順に 速度ヘッド 、 圧力ヘッド 、 位置ヘッド といいます。また、これらの和を 全ヘッド といいます。ヘッドは日本語では水頭というため、これらのことを 速度水頭 、 圧力水頭 、 位置水頭 、 全水頭 と呼ぶ場合もあります。

　ベルヌーイの定理は理想流体に対して成立するものですが、実在する流体の流れもベルヌーイの定理で説明できることが多く、さまざまな現象を理解する上で非常に重要な定理です。

 もっと知りたい  　トリチェリの定理
　図3.35に示した水槽の流出口において損失がないものとし、点1と点2でベルヌーイの定理を考えると、次の関係式が得られます。

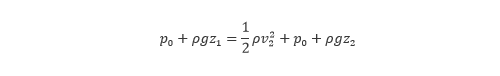
　この式を整理すると、流出する水の速度は 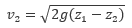となることが分かります。この関係のことを トリチェリの定理 といいます。

 もっと知りたい  　圧力のエネルギー
　圧力は単位面積あたりに作用する力で、その単位は Pa です。この Pa という単位は以下のようにも解釈することができます。

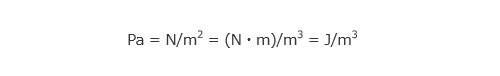
　J（= N·m）はエネルギーの単位です。このように圧力は単位体積あたりのエネルギーという見方をすることもできます。

---

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。執筆したコラムに「流体解析の基礎講座」がある。　

 

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください