4.5.4 層流熱伝達と乱流熱伝達

　乱流 では、乱れによって運動量交換が盛んに行われるため、流れに輸送される 熱量 が増加します。そのため、層流 と比較すると 熱伝達係数 が非常に大きくなります。

　 自然対流 の場合には、浮力 によって 流れ が生じます。レイノルズ数 と同じように考えると、浮力によって引き起こされる流れが層流になるか乱流になるかは、浮力と粘性力の比から見積もることができそうです。この比を表したものが グラスホフ数 と呼ばれる 無次元数 です。グラスホフ数 Gr は 重力加速度 を g [m/s²]、流体 の 体膨張率 を β [1/K]、固体 表面と 主流温度 の 温度 差を ΔT [K]、代表長さ を L [m]、流体の 動粘性係数 を ν [m² /s] を用いて、次の式で表されます。

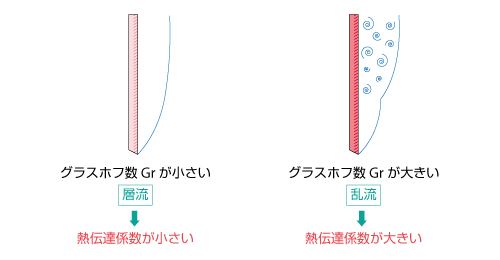
図4.17　自然対流とグラスホフ数

　熱の伝わり方は流れの状況や流速分布と温度分布の関係によって決まります。そのため、自然対流における熱の伝わりやすさは、浮力による流れの状態を表すグラスホフ数と 速度境界層 と 温度境界層 の関係を表す プラントル数 によって変化します。

　グラスホフ数とプラントル数の積を取ってひとまとめにした無次元数を レイリー数 （レイレイ数）Ra（= Gr·Pr）といい、自然対流による熱の伝わり方を整理する際によく用いられます。 レイリー数が十分小さい場合には浮力による流れは起こらず、完全な 熱伝導 によって熱が伝わります。しかし、レイリー数が大きくなるにつれて自然対流が生じ、その流れも層流から乱流へと 遷移 していきます。流れが遷移するレイリー数は対象によって異なりますが、垂直な加熱平板の場合には、Ra = 5 × 10⁸～ 3 × 10⁹が遷移域とされています。

　一方、強制対流 の場合には、流れが層流になるか乱流になるかは、レイノルズ数によって決まるため、熱の伝わり方はレイノルズ数とプラントル数によって変化します。

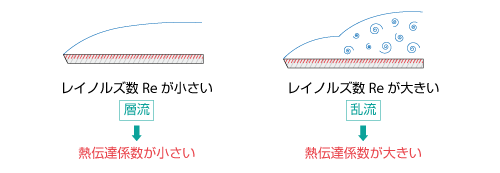
図4.18　強制対流とレイノルズ数

 もっと知りたい  　ヌセルト数

　対流熱伝達 によって、どのくらい熱が伝わりやすくなったかを表す無次元数として ヌセルト数 があります。ヌセルト数は、熱伝達係数を h [W/(m²·K)]、代表長さを L [m]、流体の 熱伝導率 を λ [W/(m·K)] とすると、次の式で定義されます。

　ヌセルト数は対流熱伝達によって運ばれる熱量と熱伝導によって運ばれる熱量の比を表したもので、完全に静止した流体（熱伝導のみによって熱が伝わる）では、Nu = 1 となります。ヌセルト数を知ることは、熱伝達係数を知ることと同じ意味がありますが、無次元数で整理されているほうが比較などの際に都合がよいことも多く、ヌセルト数の形でまとめられることがあります。

　自然対流の場合には、熱の運ばれ方はグラスホフ数とプラントル数によって決まるため、ヌセルト数はこれらの無次元数の関数となります。一方、強制対流では、レイノルズ数とプラントル数によって決まるため、ヌセルト数はこれらの無次元数の関数となります。

　ヌセルト数とこれらの無次元数の関係式が得られれば、固体の温度、流体の種類や流れの状態から伝熱量を見積もることが可能になります。しかし、伝熱量は対象の形状や位置関係など様々な要因によって複雑に変化するため、これらの関係を知ることは容易なことではありません。

---

著者プロフィール
上山 篤史 | 1983年9月 兵庫県生まれ
大阪大学大学院 工学研究科 機械工学専攻 博士後期課程修了
博士（工学）

学生時代は流体・構造連成問題に対する計算手法の研究に従事。入社後は、ソフトウェアクレイドル技術部コンサルティングエンジニアとして、既存ユーザーの技術サポートやセミナー、トレーニング業務などを担当。執筆したコラムに「流体解析の基礎講座」がある。　

 

最後までお読みいただきありがとうございます。ご意見、ご要望などございましたら、下記にご入力ください